题目内容
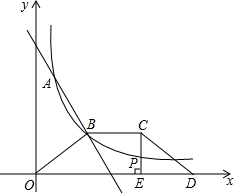
如图一次函数y=k1x+b的图象与反比例函数y=
的图象交于点A(1,6),B(3,a).
(1)求k1、k2的值;
(2)直接写出一次函数y=k1x+b的值大于反比例函数y=
的值时x的取值范围:______;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当点P为CE的中点时,求梯形OBCD的面积.
| k2 |
| x |
(1)求k1、k2的值;
(2)直接写出一次函数y=k1x+b的值大于反比例函数y=
| k2 |
| x |
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当点P为CE的中点时,求梯形OBCD的面积.

(1)把A(1,6)代入y=
,
解得,k2=6,
∴y=
,
把B(3,a)代入y=
,
解得,a=2,
∴B点坐标为(3,2),
把B(3,2)、A(1,6)代入y=k1x+b,
得3k1+b=2,k1+b=6,
解得k1=-2,b=8,
∴k1=-2,k2=6;
(2)1<x<3或x<0;
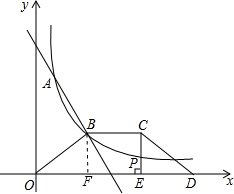 (3)如图,设C(t,2),过B作BF⊥x轴于F点,
(3)如图,设C(t,2),过B作BF⊥x轴于F点,
∵CE⊥OD于点E,点P为CE的中点,
∴P(t,1),
而点P在反比例函数y=
的图象上,
把P(t,1)代入y=
得,t=6,
∴C点坐标为(6,2),
又∵等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上且B(3,2),
∴BC=3,ED=OF=3,
∴OD=OF+EF+ED=9,而CE=2,
∴S梯形OBCD=
×(9+3)×2=12.
| k2 |
| x |
解得,k2=6,
∴y=
| 6 |
| x |
把B(3,a)代入y=
| 6 |
| x |
解得,a=2,
∴B点坐标为(3,2),
把B(3,2)、A(1,6)代入y=k1x+b,
得3k1+b=2,k1+b=6,
解得k1=-2,b=8,
∴k1=-2,k2=6;
(2)1<x<3或x<0;
 (3)如图,设C(t,2),过B作BF⊥x轴于F点,
(3)如图,设C(t,2),过B作BF⊥x轴于F点,∵CE⊥OD于点E,点P为CE的中点,
∴P(t,1),
而点P在反比例函数y=
| 6 |
| x |
把P(t,1)代入y=
| 6 |
| x |
∴C点坐标为(6,2),
又∵等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上且B(3,2),
∴BC=3,ED=OF=3,
∴OD=OF+EF+ED=9,而CE=2,
∴S梯形OBCD=
| 1 |
| 2 |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目