Question

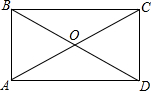
如图，矩形ABCD的两对角线AC、BD交于点O，∠AOB=60°，设AB=xcm，矩形ABCD的面积为Scm²，则变量s与x间的函数关系式为（　　）

A．s= 3 x2

B．s= 3 3 x2

C．s= 3 2 x2

D．s= 1 2 x2

Answer 1

在矩形ABCD中，AO=BO，
∵∠AOB=60°，
∴△ABO是等边三角形，
∴∠ABO=60°，
在Rt△ABD中，
∴AD=ABtan60°=

3

x，
∴矩形ABCD的面积S=AD•AB=

3

x•x=

3

x²cm²．
故选A．