Question

【题目】（2011山东济南，22，3分）如图1，△ABC中，∠C=90°，∠ABC=30°，AC=m，延长CB至点D，使BD=AB．

①求∠D的度数；

②求tan75°的值．

（2）如图2，点M的坐标为（2，0），直线MN与y轴的正半轴交于点N，∠OMN=75°．求直线MN的函数表达式．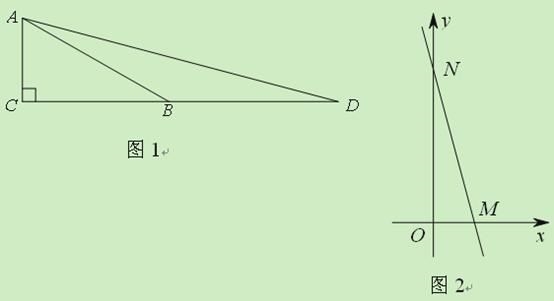

Answer 1

【答案】解：（1）①∵BD=AB，

∴∠D=∠BAD，

∴∠ABC=∠D+∠BAD=2∠D=30°，

∴∠D=15°，

②∵∠C=90°，

∴∠CAD=90°﹣∠D=90°﹣15°=75°，

∵∠ABC=30°，AC=m，

∴BD=AB=2m，BC=m，

∴cd=cb+bd=m，

∴tan∠CAD=，

∴tan75°=；

（2）∵点M的坐标为（2，0），∠OMN=75°，∠MON=90°，

∴ON=OMtan∠OMN=，

∴点N的坐标为（0，），

设直线MN的函数表达式为y=kx+b，

∴，

解得：，

∴直线MN的函数表达式为．

【解析】

（1）在直角三角形中利用角和边之间的关系求角的度数及边长即可；
（2）分别求得点M和N的坐标，利用待定系数法求函数的解析式即可．

解：（1）①∵BD=AB，

∴∠D=∠BAD，

∴∠ABC=∠D+∠BAD=2∠D=30°，

∴∠D=15°，

②∵∠C=90°，

∴∠CAD=90°﹣∠D=90°﹣15°=75°，

∵∠ABC=30°，AC=m，

∴BD=AB=2m，BC=m，

∴cd=cb+bd=m，

∴tan∠CAD=，

∴tan75°=；

（2）∵点M的坐标为（2，0），∠OMN=75°，∠MON=90°，

∴ON=OMtan∠OMN=，

∴点N的坐标为（0，），

设直线MN的函数表达式为y=kx+b，

∴，

解得：，

∴直线MN的函数表达式为．