题目内容
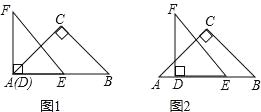
【题目】已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在BC上,(不与B、C重合),FM⊥AD,交射线AD于点M.
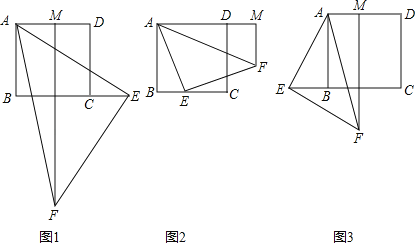
(1)如图1,当点E在边BC的延长线上,点M在边AD上时,请直接写出线段AB,BE,AM之间的数量关系,不需要证明.
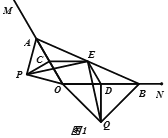
(2)如图2,当点E在边BC上,点M在边AD的延长线上时,请写出线段AB,BE,AM之间的数量关系,并且证明你的结论.
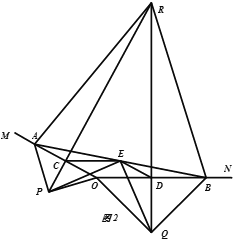
(3)如图3,当点E在边CB的延长线上,点M在边AD上时,若BE=![]() ,∠AFM=15°,求AM的长度.
,∠AFM=15°,求AM的长度.
【答案】(1)AB+AM=BE;(2)AM=BE+AB;(3)AM=3﹣![]() .
.
【解析】
(1)证明△ABE≌△EHF(AAS),可得结论:BE=AM+AB;
(2)根据AAS证明△ABE≌△EHF,可得结论:AM=BE+AB;
(3)首先由∠AFM=15°,易得∠EAB=30°,由△ABE≌△EHF,根据全等三角形的性质易得AB=EH,利用锐角三角函数易得AB,最后可以计算AM的长.
(1)AB+AM=BE.理由是:如图1,
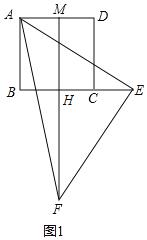
∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°
∴∠BAE+∠AEB=90°,
∵∠AEF=∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
在△ABE与△EHF中,
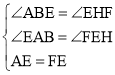 ,
,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∵FM⊥AD,
∴∠AMH=∠BAD=∠ABC=90°,
∴四边形ABHM是矩形,
∴AM=BH,
∴BE=BH+EH=AM+AB;
(2)如图2,AM=BE+AB.
证明:延长MF,交BC延长线于H,
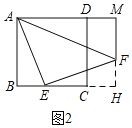
∵四边形ABCD为正方形,
∴∠BAM=∠B=90°,
∵FM⊥AD,
∴∠AMF=90°,
∴四边形ABHM为矩形,
∴AM=BH,
∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°,
∵∠B=90°,
∴∠AEB+∠BAE=90°,
∴∠FEH=∠BAE,
∵∠B=∠EHF=90°,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∴AM=BH=BE+EH=BE+AB.
(3)如图3,FM与BC相交于H.
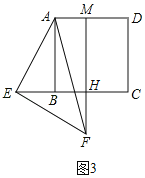
∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠EAF=45°,
同理得:四边形ABHM是矩形,
∴AM=BH,
∵AB∥FM,
∴∠BAF=∠AFM=15°,
∴∠BAE=∠EAF﹣∠BAF=45°﹣15°=30°.
在Rt△ABE中,BE=![]() ,
,
AB=![]() BE=3.
BE=3.
同理得:△ABE≌△EHF,
∴EH=AB=3,
∴BH=EH﹣BE=3﹣![]() ,
,
∴AM=BH=3﹣![]() .
.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案