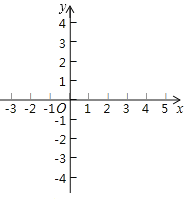ЬтФПФкШн
ЁОЬтФПЁПЯТУцЪЧаЁУїЭЌбЇЩшМЦЕФЁАвбжЊЕзБпМАЕзБпЩЯЕФИпзїЕШбќШ§НЧаЮЁБЕФГпЙцзїЭМЕФЙ§ГЬЃЎ
вбжЊЃКШчЭМ1ЃЌЯпЖЮaКЭЯпЖЮbЃЎ
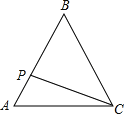
ЧѓзїЃКЁїABCЃЌЪЙЕУAB=ACЃЌBC=aЃЌBCБпЩЯЕФИпЮЊbЃЎ
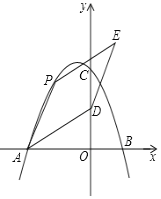
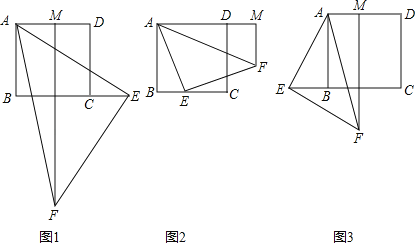
зїЗЈЃКШчЭМ2ЃЌ
ЂйзїЩфЯпBMЃЌВЂдкЩфЯпBMЩЯНиШЁBC=aЃЛ
ЂкзїЯпЖЮBCЕФДЙжБЦНЗжЯпPQЃЌPQНЛBCгкDЃЛ
ЂлвдDЮЊдВаФЃЌbЮЊАыОЖзїдВЃЌНЛPQгкAЃЛ
ЂмСЌНгABКЭACЃЎ
дђЁїABCОЭЪЧЫљЧѓзїЕФЭМаЮЃЎ
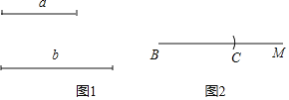
ИљОнЩЯЪізїЭМЙ§ГЬЃЌЛиД№ЮЪЬтЃК
ЃЈ1ЃЉгУжБГпКЭдВЙцЃЌВЙШЋЭМ2жаЕФЭМаЮЃЛ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃК
жЄУїЃКгЩзїЭМПЩжЊBC=aЃЌAD=bЃЎ
ЁпPQЮЊЯпЖЮBCЕФДЙжБЦНЗжЯпЃЌЕуAдкPQЩЯЃЌ
ЁрAB=ACЃЈ______ЃЉЃЈЬювРОнЃЉЃЎ
гжЁпADдкЯпЖЮBCЕФДЙжБЦНЗжЯпPQЩЯЃЌ
ЁрADЁЭBCЃЎ
ЁрADЮЊBCБпЩЯЕФИпЃЌЧвAD=bЃЎ
ЁОД№АИЁПЃЈ1ЃЉВЙЭММћНтЮіЃЛЃЈ2ЃЉЯпЖЮЕФДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮЕФСНИіЖЫЕуЕФОрРыЯрЕШ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвЊЧѓРћгУГпЙцзїГіШ§НЧаЮМДПЩЃЎ
ЃЈ2ЃЉРћгУЯпЖЮЕФДЙжБЦНЗжЯпЕФаджЪЖЈРэМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉЁїABCМДЮЊЫљЧѓЃЎ
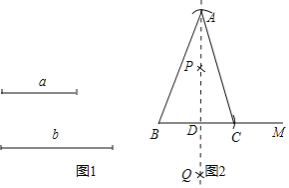
ЃЈ2ЃЉгЩзїЭМПЩжЊBC=aЃЌAD=bЃЎ
ЁпPQЮЊЯпЖЮBCЕФДЙжБЦНЗжЯпЃЌЕуAдкPQЩЯЃЌ
ЁрAB=ACЃЈЯпЖЮЕФДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮЕФСНИіЖЫЕуЕФОрРыЯрЕШЃЉЃЈЬювРОнЃЉЃЎ
гжЁпADдкЯпЖЮBCЕФДЙжБЦНЗжЯпPQЩЯЃЌ
ЁрADЁЭBCЃЎ
ЁрADЮЊBCБпЩЯЕФИпЃЌЧвAD=bЃЎ
ЙЪД№АИЮЊЃКЯпЖЮЕФДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮЕФСНИіЖЫЕуЕФОрРыЯрЕШЃЎ

 НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ
НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ
ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ