Question

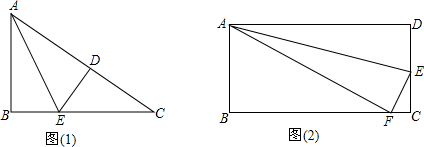
如图，在△ABC中，已知AB=2a，∠A=30°，CD是AB边的中线，若将△ABC沿CD对折起来，折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的

1

4

，有如下结论：①BC的边长等于a；②折叠前的△ABC的面积可以等于

3

3

a2；③折叠后，以A、B为端点的线段与中线CD平行且相等，其中正确的结论是______．

Answer 1

如图，设B′D与AC相交于O，
∵CD是AB边的中线，
∴S_△ACD=S_△BCD=

1

2

S_△ABC，
∵重叠部分的面积恰好等于折叠前△ABC的面积的

1

4

，
∴点O是AC、B′D的中点，
∴四边形ADCB′是平行四边形，
∴AB′∥CD，B′C∥AD，B′C=AD，故③正确；
∴B′C∥BD，B′C=BD，
∴四边形BCB′D是平行四边形，
由翻折变换的性质得，BC=B′C，
∴平行四边形BCB′D是菱形，
∴BC=BD=

1

2

AB=

1

2

×2a=a，故①正确；
假设折叠前的△ABC的面积可以等于

3

3

a²，
设点C到AB的距离为h，
则

1

2

×2ah=

3

3

a²，
解得h=

3

3

a，

3

3

a÷tan30°=

3

3

a÷

3

3

=a，
∴垂足为AB的中点D，
∴翻折后点A、B重合，不符合题意，
∴假设不成立，故②错误．
综上所述，正确的结论有①③．
故答案为：①③．