Question

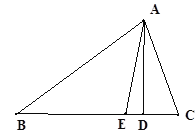
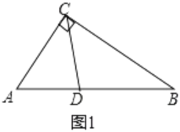
【题目】（1）如图1，在中，，，平分.

求证：.

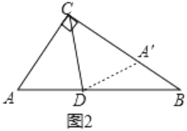
小明为解决上面的问题作了如下思考：

作关于直线的对称图形，∵平分，∴点落在上，且，.因此，要证的问题转化为只要证出即可.

请根据小明的思考，写出该问题完整的证明过程.

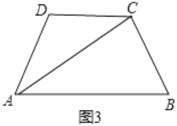
（2）参照（1）中小明的思考方法，解答下列问题：

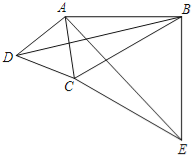
如图3，在四边形中，平分，，，，求的长.

Answer 1

【答案】（1）证明见解析；（2）21.

【解析】

（1）只需要证明，再根据等角对等边即可证明,再结合小明的分析即可证明；

（2）作△ADC关于AC的对称图形,过点C作CE⊥AB于点E，则=BE．设=BE=x．在Rt△CEB和Rt△CEA中，根据勾股定理构建方程即可解决问题.

解：（1）证明：如下图，作△ADC关于CD的对称图形△A′DC，

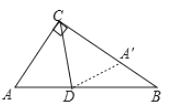
∴A′D=AD，CA′=CA，∠CA′D=∠A=60°，
∵CD平分∠ACB，
∴A′点落在CB上
∵∠ACB=90°，
∴∠B=90°-∠A=30°，

∴∠A′DB=∠CA′D-∠B=30°，即∠A′DB=∠B，

∴A′D=A′B，
∴CA+AD=CA′+A′D=CA′+A′B=CB.

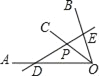
（2）如图，作△ADC关于AC的对称图形△AD′C．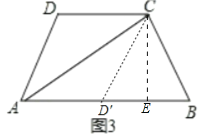

∴D′A=DA=9，D′C=DC=10，
∵AC平分∠BAD，

∴D′点落在AB上，
∵BC=10，

∴D′C=BC，
过点C作CE⊥AB于点E，则D′E=BE，
设D′E=BE=x，
在Rt△CEB中，CE2=CB2-BE2=102-x2，
在Rt△CEA中，CE2=AC2-AE2=172-（9+x）2．
∴102-x2=172-（9+x）2，
解得：x=6，
∴AB=AD′+D′E+EB=9+6+6=21．