Question

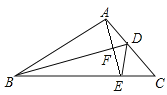
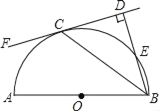
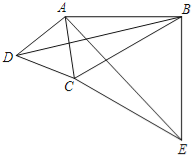
【题目】如图，在四边形ABCD中，∠ABC=30°，∠ADC=60°，AD=DC，连接AC、BD．在四边形ABCD的外部以BC为一边作等边三角形BCE，连接AE．

（1）求证：BD=AE；

（2）若AB=2，BC=3，求BD的长．

Answer 1

【答案】(1)略；（2）BD=.

【解析】

试题（1）由∠ADC=60°，AD=DC，易得△ADC是等边三角形，又由△BCE是等边三角形，可证得△BDC≌△EAC（SAS），即可得BD=AE；

（2）由△BCE是等边三角形，∠ABC=30°，易得∠ABE=90°，然后由勾股定理求得AE的长，即可求得BD的长．

试题解析：

证明：∵在△ADC中，AD=DC，∠ADC=60°，

∴△ADC是等边三角形，

∴DC=AC，∠DCA=60°；

又∵△BCE是等边三角形，

∴CB=CE，∠BCE=60°，

∴∠DCA+∠ACB=∠ECB+∠ACB，

即∠DCB=∠ACE，

在△BDC和△EAC中，

，

∴△BDC≌△EAC（SAS），

∴BD=AE；

（2）解：∵△BCE是等边三角形，

∴BE=BC=3，∠CBE=60°．

∵∠ABC=30°，

∴∠ABE=∠ABC+∠CBE=90°．

在Rt△ABE中，AE===，

∴BD=AE=．