题目内容
如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以 cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.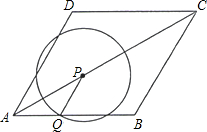 设点P运动的时间为ts.
设点P运动的时间为ts.
(1)当P异于A、C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?
 解:(1)∵四边形ABCD是菱形,且菱形ABCD的边长为2cm,
解:(1)∵四边形ABCD是菱形,且菱形ABCD的边长为2cm,∴AB=BC=2,∠BAC=
 ∠DAB,
∠DAB,又∵∠DAB=60°(已知),
∴∠BAC=∠BCA=30°;
如图1,连接BD交AC于O.

∵四边形ABCD是菱形,
∴AC⊥BD,OA=
 AC,
AC,∴OB=
 AB=1(30°角所对的直角边是斜边的一半),
AB=1(30°角所对的直角边是斜边的一半),∴OA=
 (cm),AC=2OA=2
(cm),AC=2OA=2 (cm),
(cm),运动ts后,
 ,
,∴

又∵∠PAQ=∠CAB,
∴△PAQ∽△CAB,
∴∠APQ=∠ACB(相似三角形的对应角相等),
∴PQ∥BC(同位角相等,两直线平行)
(2)如图2,⊙P与BC切于点M,连接PM,则PM⊥BC.
在Rt△CPM中,∵∠PCM=30°,∴PM=
 PC=
PC=
由PM=PQ=AQ=t,即
 =t
=t解得t=4
 -6,此时⊙P与边BC有一个公共点;
-6,此时⊙P与边BC有一个公共点;如图3,⊙P过点B,此时PQ=PB,
∵∠PQB=∠PAQ+∠APQ=60°
∴△PQB为等边三角形,∴QB=PQ=AQ=t,∴t=1
∴
 时,⊙P与边BC有2个公共点.
时,⊙P与边BC有2个公共点.如图4,⊙P过点C,此时PC=PQ,即2

 t=t,∴t=3-
t=t,∴t=3- .
.∴当1<t≤3-
 时,⊙P与边BC有一个公共点,
时,⊙P与边BC有一个公共点,当点P运动到点C,即t=2时,⊙P过点B,此时,⊙P与边BC有一个公共点,
∴当t=4
 -6或1<t≤3-
-6或1<t≤3- 或t=2时,⊙P与菱形ABCD的边BC有1个公共点;
或t=2时,⊙P与菱形ABCD的边BC有1个公共点;当4
 -6<t≤1时,⊙P与边BC有2个公共点.
-6<t≤1时,⊙P与边BC有2个公共点.分析:(1)连接BD交AC于O,构建直角三角形AOB.利用菱形的对角线互相垂直、对角线平分对角、邻边相等的性质推知△PAQ∽△CAB;然后根据“相似三角形的对应角相等”证得∠APQ=∠ACB;最后根据平行线的判定定理“同位角相等,两直线平行”可以证得结论;
(2)如图2,⊙P与BC切于点M,连接PM,构建Rt△CPM,在Rt△CPM利用特殊角的三角函数值求得PM=
 PC=
PC= ,然后根据PM=PQ=AQ=t列出关于t的方程,通过解方程即可求得t的值;
,然后根据PM=PQ=AQ=t列出关于t的方程,通过解方程即可求得t的值;如图3,⊙P过点B,此时PQ=PB,根据等边三角形的判定可以推知△PQB为等边三角形,然后由等边三角形的性质以及(2)中求得t的值来确定此时t的取值范围;
如图4,⊙P过点C,此时PC=PQ,据此等量关系列出关于t的方程,通过解方程求得t的值.
点评:本题综合考查了菱形的性质、直线与圆的位置关系以及相似三角形的判定等性质.解答(2)题时,根据⊙P的运动过程来确定t的值,以防漏解.

练习册系列答案
相关题目
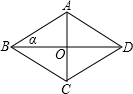 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
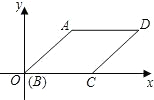 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.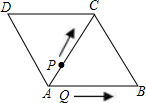 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).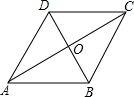 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.