题目内容
 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.(1)求出经过A、D、C三点的抛物线解析式;
(2)是否存在时刻t使得PQ⊥DB,若存在请求出t值,若不存在,请说明理由;
(3)设AE长为y,试求y与t之间的函数关系式;
(4)若F、G为DC边上两点,且点DF=FG=1,试在对角线DB上找一点M、抛物线ADC对称轴上找一点N,使得四边形FMNG周长最小并求出周长最小值.
分析:(1)求抛物线的解析式可利用待定系数法,关键在于确定点D、C的坐标.在等边△DAB中,已知边长,容易求出点D到x、y轴的距离,据此可得点D的坐标.而将点D向右平移6个单位就能得到点C的坐标,则此问可解.
(2)菱形的对角线互相垂直平分,那么连接AC后,则有AC⊥DB,若PQ⊥DB,必须满足PQ∥AC,显然当点P在BC上时是不会符合该条件的,那么只有P在CD上这一种情况.此时,四边形PCAQ是平行四边形,由对边相等(即PC=AQ)列等式即可求出t值.
(3)此问应分作两段分析:
①P在CD上,此时AQ∥DP,有△DEP∽△AEQ,利用对应边成比例可求出AE、DE的比例关系,由此得到y的表达式;
②P在BC上,此时AE∥PB,有△QEA∽△QPB,解题思路同①,利用相似三角形的性质得到y的表达式.
(4)要注意两条关键线:直线BD、抛物线的对称轴;若使得四边形FMNG的周长最小,可先作F、G分别关于直线BD、抛物线对称轴的对称点F′、G′,连接F′G′后,与BD、对称轴的交点就是符合条件的M、N,那么四边形的最小周长即为F′G′+FG.
(2)菱形的对角线互相垂直平分,那么连接AC后,则有AC⊥DB,若PQ⊥DB,必须满足PQ∥AC,显然当点P在BC上时是不会符合该条件的,那么只有P在CD上这一种情况.此时,四边形PCAQ是平行四边形,由对边相等(即PC=AQ)列等式即可求出t值.
(3)此问应分作两段分析:
①P在CD上,此时AQ∥DP,有△DEP∽△AEQ,利用对应边成比例可求出AE、DE的比例关系,由此得到y的表达式;
②P在BC上,此时AE∥PB,有△QEA∽△QPB,解题思路同①,利用相似三角形的性质得到y的表达式.
(4)要注意两条关键线:直线BD、抛物线的对称轴;若使得四边形FMNG的周长最小,可先作F、G分别关于直线BD、抛物线对称轴的对称点F′、G′,连接F′G′后,与BD、对称轴的交点就是符合条件的M、N,那么四边形的最小周长即为F′G′+FG.
解答:解:(1)△DAB中,∠DAB=60°,DA=AB=6
则:D到y轴的距离=
AB=3、D到x轴的距离=DA•sin∠DAB=3
;
∴D(3,3
);
由于DC∥x轴,且DC=AB=6,那么将点D右移6个单位后可得点C,即C(9,3
);
设抛物线的解析式为:y=ax2+bx,有:
,解得
∴抛物线解析式为:y=-
x2+
x.
(2)如图1,连接AC知AC⊥BD,若PQ⊥DB,则PQ∥AC,那么P在BC上时不存在符合要求的t值,
当P在DC上时,由于PC∥AQ且PQ∥AC,
所以四边形PCAQ是平行四边形,
则PC=AQ,有6-2t=t,得t=2.
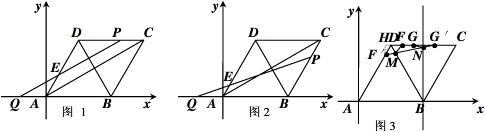 (3)①如图1,当点P在DC上,即0≤t≤3时,
(3)①如图1,当点P在DC上,即0≤t≤3时,
有△EDP∽△EAQ,
则
=
=
=
,
那么AE=
AD=2,即y=2;
②如图2,当点P在CB上,
即3<t≤6时,有△QEA∽△QPB,
则
=
,即
=
,
得y=
,
综上所述:y=
,
(4)如图3,作点F关于直线DB的对称点F′,由菱形对称性知F′在DA上,用DF′=DF=1;
作点G关于抛物线ADC对称轴的对称点G′,
易求DG′=4,
连接F′G′交DB于点M、交对称轴于点N,点M、N即为所求的两点.
过F′作F′H⊥DG′于H,
在Rt△F′HD中,∠F′DH=180°-∠ADC=60°,F′D=1;
则:F′H=F′D•sin60°=
,HD=F′D•cos60°=
,HG′=HD+DG′=
.
用勾股定理计算得F′G′=
,所以四边形FMNG周长最小为F′G′+FG=
+1.
则:D到y轴的距离=
| 1 |
| 2 |
| 3 |
∴D(3,3
| 3 |
由于DC∥x轴,且DC=AB=6,那么将点D右移6个单位后可得点C,即C(9,3
| 3 |
设抛物线的解析式为:y=ax2+bx,有:
|
|
∴抛物线解析式为:y=-
| 1 |
| 9 |
| 3 |
| 4 |
| 3 |
| 3 |
(2)如图1,连接AC知AC⊥BD,若PQ⊥DB,则PQ∥AC,那么P在BC上时不存在符合要求的t值,
当P在DC上时,由于PC∥AQ且PQ∥AC,
所以四边形PCAQ是平行四边形,
则PC=AQ,有6-2t=t,得t=2.
 (3)①如图1,当点P在DC上,即0≤t≤3时,
(3)①如图1,当点P在DC上,即0≤t≤3时,有△EDP∽△EAQ,
则
| AE |
| DE |
| AQ |
| DP |
| t |
| 2t |
| 1 |
| 2 |
那么AE=
| 1 |
| 3 |
②如图2,当点P在CB上,
即3<t≤6时,有△QEA∽△QPB,
则
| AE |
| PB |
| AQ |
| QB |
| AE |
| 12-2t |
| t |
| 6+t |
得y=
| 2t(6-t) |
| 6+t |
综上所述:y=
|
(4)如图3,作点F关于直线DB的对称点F′,由菱形对称性知F′在DA上,用DF′=DF=1;
作点G关于抛物线ADC对称轴的对称点G′,
易求DG′=4,
连接F′G′交DB于点M、交对称轴于点N,点M、N即为所求的两点.
过F′作F′H⊥DG′于H,
在Rt△F′HD中,∠F′DH=180°-∠ADC=60°,F′D=1;
则:F′H=F′D•sin60°=
| ||
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
用勾股定理计算得F′G′=
| 21 |
| 21 |
点评:此题为函数几何综合解答题,涉及了二次函数、特殊四边形、相似三角形、勾股定理、轴对称性等有关知识,也重点考查了学生对分类讨论思想的掌握情况.本题着力菱形的各项性质而设计,如“菱形的对角线互相垂直”、“菱形对边互相平行”、“菱形是轴对称图形”等,(2)(3)(4)问依次考察了学生对菱形基本性质的掌握程度及运用其性质灵活解题的能力,本题在设计时,(1)(2)(3)(4)问难度依次递增,充分考虑了不同层次的学生,让每位答题的学生都有所收获,都能获取成功的体验,同时本题又兼顾了压轴题的选拔功能,通过本题可以很好地区分学生的层次,激发更多的学生去攀登数学高峰.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
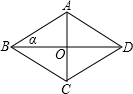 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
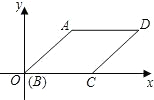 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为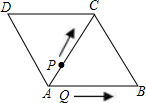 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形). 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.