题目内容
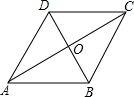 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.分析:根据菱形的四条边都相等求出菱形的边长,再根据菱形的邻角互补求出∠BAD=60°,然后求出△ABD是等边三角形,从而得到BD的长,根据菱形的对角线互相BAD垂直平分求出AO的长,从而得到AC的长.
解答:解:∵菱形ABCD的周长为8cm,
∴菱形的边长为8÷4=2cm,
∵∠ABC:∠BAD=2:1,∠ABC+∠BAD=180°(菱形的邻角互补),
∴∠BAD=
×180°=60°,
∴△ABD是等边三角形,
∴BD=2cm,
∵菱形ABCD对角线AC、BD相交于点O,
∴AO=CO,BO=DO=1且AC⊥BD,
∴AO=
=
=
,
∴AC=2AO=2
.
故答案为:BD=2,AC=2
.
∴菱形的边长为8÷4=2cm,
∵∠ABC:∠BAD=2:1,∠ABC+∠BAD=180°(菱形的邻角互补),
∴∠BAD=
| 1 |
| 1+2 |
∴△ABD是等边三角形,
∴BD=2cm,
∵菱形ABCD对角线AC、BD相交于点O,
∴AO=CO,BO=DO=1且AC⊥BD,
∴AO=
| AC2-DO2 |
| 22-12 |
| 3 |
∴AC=2AO=2
| 3 |
故答案为:BD=2,AC=2
| 3 |
点评:本题考查了菱形的性质,主要利用了菱形的四条边都相等,邻角互补,对角线互相垂直平分的性质,证明得到△ABD是等边三角形是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
 22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.
22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.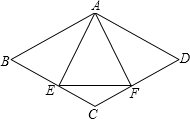 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF; (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.