题目内容
如图,菱形ABCD的边长为8cm,∠B=60°,P、Q同时从A点出发,点P以1cm/秒的速度沿A→C→B的方向运动,点Q以2cm/秒的速度沿A→B→C→D的方向运动.当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为x秒,△APQ与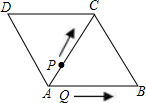 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
(1)当x=
(2)当x=
(3)当x=
秒时,△APQ是等边三角形;
(4)求y关于x的函数关系式,并求y的最大值.
 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).(1)当x=
8
8
秒时,P和Q相遇;(2)当x=
(12-4
)
| 3 |
(12-4
)
秒时,△APQ是等腰直角三角形;| 3 |
(3)当x=
| 32 |
| 3 |
| 32 |
| 3 |
(4)求y关于x的函数关系式,并求y的最大值.
分析:(1)菱形ABCD的边长为8cm,∠B=60°,则易证△ABC是等边三角形,且边长是8cm.由点P、Q从出发到相遇,则两人所走的路程的和是24cm.设从出发到相遇所用的时间是x秒,据此列方程,求解即可;
(2)当P在AC上,Q在AB上时,由于∠PAQ=60°,则△APQ一定不是等腰直角三角形;当P在AC上,Q在BC上时,若△APQ是等腰直角三角形,由于∠PAQ<60°,即△APQ中A点不能为直角顶点,如果∠PQA=90°,则∠PAQ=45°,∠QAB=15°,而∠B=60°,所以∠CQA=75°<∠PQA,不合题意,即△APQ中Q点不能为直角顶点,所以只能∠APQ=90°,AP=PQ,根据这个相等关系,就可以得到一个关于x的方程,就可以得到x的值;当P在BC上,Q在CD上时,△APQ一定不是等腰直角三角形;
(3)当P在AC上,Q在AB上时,AP≠AQ,则△APQ一定不是等边三角形;当P在AC上,Q在BC上时,∠PAQ<60°,则△APQ一定不是等边三角形;当P在BC上,Q在CD上时,若△APQ是等边三角形,则易证△ADQ≌△ACP,得出CP=DQ,根据这个相等关系,就可以得到一个关于x的方程,解方程即可求出x的值;
(4)求y与x之间的函数关系式,应根据0≤x≤4和4<x≤8以及8<x≤12三种情况进行讨论.把x当作已知数值,就可以求出y,即可得到函数的解析式.
(2)当P在AC上,Q在AB上时,由于∠PAQ=60°,则△APQ一定不是等腰直角三角形;当P在AC上,Q在BC上时,若△APQ是等腰直角三角形,由于∠PAQ<60°,即△APQ中A点不能为直角顶点,如果∠PQA=90°,则∠PAQ=45°,∠QAB=15°,而∠B=60°,所以∠CQA=75°<∠PQA,不合题意,即△APQ中Q点不能为直角顶点,所以只能∠APQ=90°,AP=PQ,根据这个相等关系,就可以得到一个关于x的方程,就可以得到x的值;当P在BC上,Q在CD上时,△APQ一定不是等腰直角三角形;
(3)当P在AC上,Q在AB上时,AP≠AQ,则△APQ一定不是等边三角形;当P在AC上,Q在BC上时,∠PAQ<60°,则△APQ一定不是等边三角形;当P在BC上,Q在CD上时,若△APQ是等边三角形,则易证△ADQ≌△ACP,得出CP=DQ,根据这个相等关系,就可以得到一个关于x的方程,解方程即可求出x的值;
(4)求y与x之间的函数关系式,应根据0≤x≤4和4<x≤8以及8<x≤12三种情况进行讨论.把x当作已知数值,就可以求出y,即可得到函数的解析式.
解答:解:(1)∵四边形ABCD是菱形,
 ∴AB=BC=8cm,
∴AB=BC=8cm,
又∵∠B=60°,
∴△ABC是等边三角形.
设点P,Q从出发到相遇所用的时间是x秒.
根据题意,得x+2x=24,
解得x=8秒.
即当x=8秒时,P和Q相遇;
 (2)若△APQ是等腰直角三角形,则此时点P在AC上,点Q在BC上,如图.
(2)若△APQ是等腰直角三角形,则此时点P在AC上,点Q在BC上,如图.
∵△APQ是等腰直角三角形,∴∠APQ=90°,∴∠CPQ=90°.
∵AP=x,∴CP=AC-AP=8-x.
在△CPQ中,∵∠CPQ=90°,∠PCQ=60°,∴∠CQP=30°,
∴PQ=
CP=
(8-x).
∵△APQ是等腰直角三角形,∠APQ=90°,∴AP=PQ,
即x=
(8-x),
解得x=12-4
.
故当x=(12-4
)秒时,△APQ是等腰直角三角形;
 (3)若△APQ是等边三角形,则此时点P在BC上,点Q在CD上,如图.
(3)若△APQ是等边三角形,则此时点P在BC上,点Q在CD上,如图.
且△ADQ≌△ACP,则CP=DQ,
即x-8=24-2x,解得x=
.
故当x=
秒时,△APQ是等边三角形;
(4)分三种情况讨论:
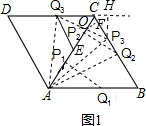 ①当0≤x≤4时,
①当0≤x≤4时,
y=S△AP1Q1=
AP1×AQ1×sin60°=
x•2x×
=
x2,
根据二次函数的性质,可知当x=4时,y有最大值
×16=8
;
②当4<x≤8时,
y=S△AP2Q2=
AP2×CQ2sin60°
=
x(16-2x)×
=-
x2+4
x,
根据二次函数的性质,可知当4<x≤8时,y无最大值;
③当8<x≤12时,设P3Q3与AC交于点O.
过Q3作Q3E∥CB,则△CQ3E为等边三角形.
∴Q3E=CE=CQ3=2x-16.
∵Q3E∥CB,
∴△COP3∽△EOQ3,
∴OC:OE=CP3:EQ3=(x-8):(2x-16)=1:2,
∴OC=
CE=
(2x-16).
∴y=S△AOP3=S△ACP3-S△COP3=
CP3×ACsin60°-
OC×CP3sin60°
=
(x-8)×8×
-
×
(2x-16)(x-8)×
=-
x2+
x-
,
根据二次函数的性质,可知当x=12时,y有最大值-
×122+
×12-
=
.
综上可知,当x=4时,y有最大值
×16=8
.
故答案为8,(12-4
),
.
 ∴AB=BC=8cm,
∴AB=BC=8cm,又∵∠B=60°,
∴△ABC是等边三角形.
设点P,Q从出发到相遇所用的时间是x秒.
根据题意,得x+2x=24,
解得x=8秒.
即当x=8秒时,P和Q相遇;
 (2)若△APQ是等腰直角三角形,则此时点P在AC上,点Q在BC上,如图.
(2)若△APQ是等腰直角三角形,则此时点P在AC上,点Q在BC上,如图.∵△APQ是等腰直角三角形,∴∠APQ=90°,∴∠CPQ=90°.
∵AP=x,∴CP=AC-AP=8-x.
在△CPQ中,∵∠CPQ=90°,∠PCQ=60°,∴∠CQP=30°,
∴PQ=
| 3 |
| 3 |
∵△APQ是等腰直角三角形,∠APQ=90°,∴AP=PQ,
即x=
| 3 |
解得x=12-4
| 3 |
故当x=(12-4
| 3 |
 (3)若△APQ是等边三角形,则此时点P在BC上,点Q在CD上,如图.
(3)若△APQ是等边三角形,则此时点P在BC上,点Q在CD上,如图.且△ADQ≌△ACP,则CP=DQ,
即x-8=24-2x,解得x=
| 32 |
| 3 |
故当x=
| 32 |
| 3 |
(4)分三种情况讨论:
 ①当0≤x≤4时,
①当0≤x≤4时,y=S△AP1Q1=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
根据二次函数的性质,可知当x=4时,y有最大值
| ||
| 2 |
| 3 |
②当4<x≤8时,
y=S△AP2Q2=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
根据二次函数的性质,可知当4<x≤8时,y无最大值;
③当8<x≤12时,设P3Q3与AC交于点O.
过Q3作Q3E∥CB,则△CQ3E为等边三角形.
∴Q3E=CE=CQ3=2x-16.
∵Q3E∥CB,
∴△COP3∽△EOQ3,
∴OC:OE=CP3:EQ3=(x-8):(2x-16)=1:2,
∴OC=
| 1 |
| 3 |
| 1 |
| 3 |
∴y=S△AOP3=S△ACP3-S△COP3=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
14
| ||
| 3 |
80
| ||
| 3 |
根据二次函数的性质,可知当x=12时,y有最大值-
| ||
| 6 |
14
| ||
| 3 |
80
| ||
| 3 |
16
| ||
| 3 |
综上可知,当x=4时,y有最大值
| ||
| 2 |
| 3 |
故答案为8,(12-4
| 3 |
| 32 |
| 3 |
点评:本题借助动点问题考查了菱形的性质,等边三角形的性质,等腰直角三角形的性质,相似三角形的判定与性质,三角形的面积,求函数的解析式及最值,综合性较强,难度较大.注意运用分类讨论及数形结合的思想是解决本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
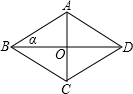 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
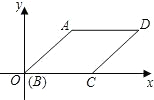 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.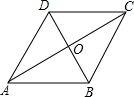 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.