题目内容
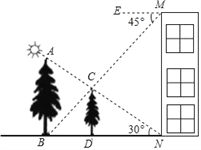
【题目】如图，在楼房MN前有两棵树与楼房在同一直线上，且垂直于地面，为了测量树AB、CD的高度，小明爬到楼房顶部M处，光线恰好可以经过树CD的顶站C点到达树AB的底部B点，俯角为45°，此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点，与地面的夹角为30°，树CD的影长DN为15米，请求出树AB、CD的高度．（结果保留根号）
【答案】树高AB是（5+5
）米，树高CD是5
米．
【解析】试题分析: 在Rt△CDN中，由于tan30°=
，得到CD=tan30°DN=5
于是得到BD=CD=5
，在Rt△ABN中，根据三角函数的定义即可得到结论．
试题解析:
在Rt△CDN中，
∵tan30°=
，
∴CD=tan30°DN=5
，
∵∠CBD=∠EMB=45°，
∴BD=CD=5
，
∴BN=DN+BD=15+5
，
在Rt△ABN中，tan30°=
，
∴AB=tan30°BN=5+5
，
∴树高AB是（5+5
）米，树高CD是5
米．
练习册系列答案
相关题目
