题目内容
【题目】定义:点P为△ABC内部或边上的点,若满足△PAB,△PBC,△PAC至少有一个三角形与△ABC相似(点P不与△ABC顶点重合),则称点P为△ABC的自相似点.

例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
(1)点A坐标为(![]() ,
, ![]() ), AB⊥x轴于B点,在E(2,1),F (
), AB⊥x轴于B点,在E(2,1),F (![]() ,
, ![]() ),G (
),G (![]() ,
, ![]() ),这三个点中,其中是△AOB的自相似点的是 (填字母);
),这三个点中,其中是△AOB的自相似点的是 (填字母);
(2)若点M是曲线C: ![]() (
(![]() ,
, ![]() )上的一个动点,N为x轴正半轴上一个动点;
)上的一个动点,N为x轴正半轴上一个动点;
 图2
图2
① 如图2, ![]() ,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
②若![]() ,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).

【答案】(1)F,G(2)①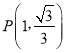 或
或 ②4
②4
【解析】试题分析:(1)如图,连接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.只要证明△OBG∽△OAB,可得点G是自相似点,△FOB∽△BAO,可得点F是自相似点.
(2)①如图1,过点M作MH⊥x轴于H点.将M的横坐标代入反比例函数解析式求出点M的坐标和OM的长,进而求出直线OM的解析式.在Rt△MHN中,根据勾股定理求出ON=MN=m=2.如图2, ![]() ∽
∽![]() ,过点
,过点![]() 作
作![]() ⊥x轴于Q点,由相似的性质得出
⊥x轴于Q点,由相似的性质得出![]() ,
, ![]() .得出P1的横坐标为1,代入OM解析式求出即可求出P1的坐标;如图3,
.得出P1的横坐标为1,代入OM解析式求出即可求出P1的坐标;如图3, ![]() ,根据相似三角形的性质求出P2N的长,进而可得P2的坐标.
,根据相似三角形的性质求出P2N的长,进而可得P2的坐标.
②以O为圆心2为半径作圆交反比例函数于M1,M2,以N为圆心2为半径作圆交反比例函数的图象于M3,M4.满足条件的点M有4个.
试题解析:
解:(1)如图中,连接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.
由题意可知点G在OA上,
∵tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
∵tan∠GBM=![]() =
=![]() =
=![]() ,
,
∴∠OBG=30°,
∴∠BOG=∠AOB,∠OBG=∠A,
∴△OBG∽△OAB,
∴点G是自相似点,
同理可得∠FON=∠A=30°,∠FBO=∠AOB=60°,
∴△FOB∽△BAO,
∴点F是自相似点,
span>故答案为F,G;
(2)①如图1,过点M作MH⊥x轴于H点.
∵M点的横坐标为3,
∴![]() .
.
∴![]() .
.
∴![]() ,直线OM的表达式为
,直线OM的表达式为![]() .
.
∵MH⊥x轴,
∴在Rt△MHN中, ![]() °,
°,![]() .
.
设NM=NO=m,则![]() .
.
∴![]() .
.
∴ON=MN=m=2.
如图2, ![]() ∽
∽![]() ,过点
,过点![]() 作
作![]() ⊥x轴于Q点,
⊥x轴于Q点,

∴![]() ,
, ![]() .
.
∵![]() 的横坐标为1,
的横坐标为1,
∴![]() .
.
∴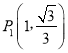 .
.
如图3, ![]() ,
,

∴![]() .
.
∴![]() .
.
∵![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() .
.
∴![]() .
.
∴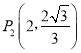 .
.
综上所述, 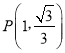 或
或 .
.
②以O为圆心2为半径作圆交反比例函数于M1,M2,以N为圆心2为半径作圆交反比例函数的图象于M3,M4.满足条件的点M有4个.
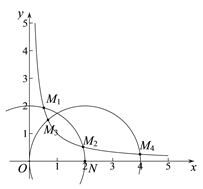
故答案为4.

 阅读快车系列答案
阅读快车系列答案【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .