Question

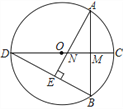
【题目】如图，边长为4的正方形ABCD外有一点E，∠AEB＝90°，F为DE的中点，连接CF，则CF的最大值为___________

Answer 1

【答案】+1

【解析】连接BD，取BD、AD的中点为H、G，连接FH、GF，

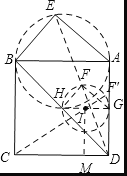
∵F为DE的中点，

∴FH是△BDE的中位线，FG是△ADE的中位线，

∴FH∥BE,FG∥AE，

∴∠HFD=∠BED，∠GFD=∠AED，

∵∠AEB=90°，

∴∠BED+∠AED=90°，

∴∠HFD+∠GFD=90°，

∴∠HFG=90°，

∴点F在以GH为直径的半圆上运动，

取GH的中点I，

则CF最大时，是经过圆心I，

∵GH是△ABD的中位线，

∴GH=AB=×4=2，

∴GI=1，

过I作IM⊥CD于M，

在Rt△CIM中，CM=41=3，IM=2，

由勾股定理得：CI=，

∴CF′=，

故答案为： .