题目内容
【题目】如图,已知长方形纸片ABCD,AB=4,BC=10,M是BC的中点,点P沿折线BA—AD运动,以MD为折瘪将长方形纸片向右翻折,使点B落在长方形的AD边上,则折痕MP的长______.

【答案】![]() 或
或![]() 或4
或4
【解析】
分三种情况进行讨论:①点B′落在AB边上,②点B′落在AD边上,③点B′与点C重合,根据折叠的性质,分别画出图形进行求解.
解:①如图,当点B′落在AB边上时,过M作ME⊥AD于E,可得四边形ABME为矩形,
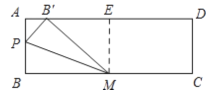
∴EM=AB=4,AE=BM,
又∵BC=10,M为BC的中点,
∴由折叠可得:B′M=BM=AE=5,
在Rt△EMB′中,根据勾股定理得:B′E=![]() ,
,
∴AB′=AEB′E=2,
设BP=x,则AP=4x,PB′=x,
在Rt△PAB′中,根据勾股定理得:PB′=AP+AB′,
即x=(4x)+2,
解得x=![]() ,
,
∴PB=![]() ,
,
在Rt△BMP中,根据勾股定理得:PM=![]() ;
;
②如图,当点B′落在AD边上时,过M作ME⊥AD于E,可得四边形ABME为矩形,

∴EM=AB=4,
又∵BC=10,M为BC的中点,
∴由折叠可得:B′M=BM=5,
在Rt△EMB′中,根据勾股定理得:B′E=![]()
由AD∥BC可得,∠DPM=∠BMP,
由折叠可得,∠PMB′=∠BMP,
∴∠DPM=∠PMB′,
∴B′M=B′P=5,
∴PE=53=2,
在Rt△PEM中,根据勾股定理得:PM=![]() ;
;
③如图,当点B′与点C重合时,由∠A=∠B=∠BMP=90°,可得四边形ABMP为矩形,
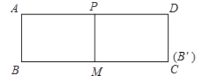
此时,PM=AB=4.
综上所述,折痕MP的长为:![]() 或
或![]() 或4.
或4.
故答案为:![]() 或
或![]() 或4.
或4.

 阅读快车系列答案
阅读快车系列答案【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .





