题目内容
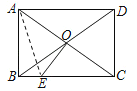
【题目】如图，矩形ABCD中，AD＝4，对角线AC与BD交于点O，OE⊥AC交BC于点E，CE＝3，则矩形ABCD的面积为（ ）
A.
B.
C.12D.32
【答案】B
【解析】
要求矩形的面积，已知一边的长度，所以只要把邻边的长度求出即可．因为矩形的对角线相互平分，所以点O是AC的中点，又因为OE垂直AC，所以OE是AC的垂直平分线，见到垂直平分线，我们应该想到垂直平分线的性质，根据垂直平分线的性质：垂直平分线上的点到线段两端距离相等，所以需要连接AE，可得AE=EC,再根据勾股定理可求出AB的长度，则矩形的面积就可以算出了．
如图连接AE
矩形的对角线相互平分
O为AC的中点
又 OE
AC
OE是AC的垂直平分线
AE=EC=3,BE=BC-EC=AD-EC=1
是直角三角形，由勾股定理可得：
AB=
矩形ABCD的面积=
故本题选B． 
练习册系列答案
名校课堂系列答案
相关题目
