题目内容
【题目】如图,等边 ABC 的边长是 2 , D 、 E 分别为 AB 、 AC 的中点,连接CD ,过 E 点作 EF // DC 交 BC 的延长线于点 F
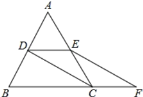
(1) 求证:四边形 CDEF 是平行四边形;
(2)求四边形 CDEF 的周长
【答案】(1)见解析;(2)2+2![]() .
.
【解析】
(1)直接利用三角形中位线定理得出DE∥BC,再利用平行四边形的判定方法得出答案;
(2)利用等边三角形的性质结合平行四边形的性质得出DC=EF,进而求出答案.
(1)证明:∵D、E分别是AB,AC中点,
∴DE∥BC,DE=![]() BC=1
BC=1
∵EF // DC
∴四边形CDEF是平行四边形,
(2)∵四边形DEFC是平行四边形,
∴DC=EF,DE=CF
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=![]()
∴四边形CDEF的周长是2+2![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目