��Ŀ����
����Ŀ���ٺ��г��е���������Ϊ�˷ḻѧ����������֯ͬѧ��չÿ��һ�ε����Ż����������������������衢�������干5�Ϊ������֯���涨ÿλͬѧֻ�ܱ�һ�������ݱ������������������в�������ͳ��ͼ������������⣺ 
��1��������ͳ��ͼ����������
��2��д������ͳ��ͼ�е�m��n��ֵ��
��3����������������ͬѧ���������������������ܸ���Ȥ�������������������ȡһ��μӣ�������״ͼ���б���ʾ���п��ܽ������������˲μ�ͬһ��Ŀ�ĸ��ʣ�
��4�����ڳ������ƣ��μ�������ѧ���������ܳ����μ�����ѧ�������� ![]() ����ô���ټ�λͬѧ��Ҫ�Ӳμ������������μ�������
����ô���ټ�λͬѧ��Ҫ�Ӳμ������������μ�������
���𰸡�
��1���⣺���ε����ѧ������Ϊ60��20%=300���ˣ���
��ѡ����������ѧ����300����60+50+30+120��=40���ˣ���
��ȫͼ��Ϊ��
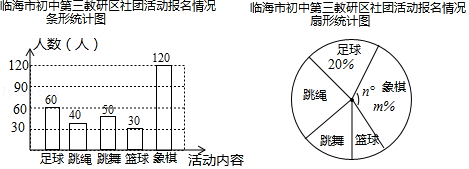
��2���⣺����ͳ��ͼ��������ռ�ٷֱ�Ϊm%= ![]() ��100%=40%����Բ�ĽǶ���Ϊ360���40%=144�㣬
��100%=40%����Բ�ĽǶ���Ϊ360���40%=144�㣬
��m=40��n=144��
��3���⣺�������������������ֱ�ΪA��B��C��
����״ͼ�ã�
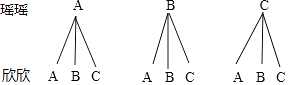
���������P��ͬһ����= ![]() =
= ![]() ��
��
��4���⣺��xλͬѧ�Ӳμ�������Ŀ������������Ŀ��
�������⣬�ã�60��x�� ![]() ��240+x����
��240+x����
��ã�x��17 ![]() ��
��
��x������
��������Ҫ18λѧ����������
����������1����������������ٷֱ�������������ټ�ȥ���������ɵ��������������ɲ�ȫ����ͼ����2�����������������������ɵðٷֱȣ��ٳ���360�ȿɵ�n��ֵ����3������״ͼ�г����еȿ��ܽ�������ҵ�ͬһ��Ľ���������ݸ��ʹ�ʽ�ɵô𰸣���4����xλͬѧ�Ӳμ�������Ŀ������������Ŀ�����ݡ��μ�������ѧ���������ܳ����μ�����ѧ�������� ![]() ���в���ʽ���ɵã�
���в���ʽ���ɵã�
�����㾫����������Ŀ����֪��������������ͳ��ͼ������ͳ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�