题目内容
【题目】综合题。
(1)计算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
【答案】
(1)解:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]()
=1+2+2 ![]()
=3;
(2)解: ![]() ÷(
÷( ![]() ﹣x+1)
﹣x+1)
= ![]()
= ![]()
= ![]() ,
,
∵﹣tan60°≤x≤2cos30°
∴ ![]() ,
,
∴当x=1时,原式= ![]() =﹣1.
=﹣1.
【解析】(1)根据零指数幂、负整数指数幂、绝对值可以解答本题;(2)先化简题目中的式子,然后根据﹣tan60°≤x≤2cos30°,从中选取使得原分式有意义的x的整数值代入即可解答本题.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握整数指数幂的运算性质(aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数))的相关知识才是答题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
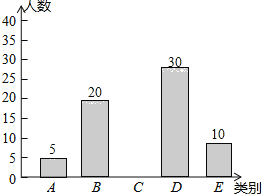
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.