题目内容

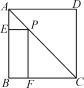
【题目】如图，P为正方形ABCD的对角线AC上任意一点，PE⊥AB于E，PF⊥BC于F，若AC＝，则四边形PEBF的周长为( )

A. B. 2 C. 2 D. 1

【答案】C

【解析】

由题中条件可得四边形FBFP为矩形，又点P在对角线上，可得PE=AE，进而可求其周长等于正方形的边长的2倍，根据勾股定理，可得四边形的边长为1，所以四边形PEBF的周长为2.

由题意可得，四边形EBFP为矩形，所以BF=PE，PF=BE，又点P在对角线AC上，∠BAC=45°，所以AE=PE，所以四边形PEBF的周长为BE+EP+PF+BF=BE+AE+PF+AE=2AB.

∵AC=，AB=BC，

∴2AB2=AC2，即2AB2=2，

∴AB=1，

∴四边形PEBF的周长为2AB=2.

故选C.

练习册系列答案
相关题目

【题目】点A1、A2、A3、…、An（n为正整数）都在数轴上．点A2在点A1的左边，且A1A2=1；点A3在点A2的右边，且A2A3=2；点A4在点A3的左边，且A3A4=3；…，点A2018在点A2017的左边，且A2017A2018=2017，若点A2018所表示的数为2018，则点A1所表示的数为_____．

【题目】临海市初中第三教研区为了丰富学生课余活动，组织同学开展每周一次的社团活动，活动内容有足球、跳绳、跳舞、篮球、象棋共5项，为方便组织，规定每位同学只能报一项活动，根据报名绘制了如下两幅尚不完整的统计图，解答下列问题：
（1）将条形统计图补充完整；
（2）写出扇形统计图中的m和n的值；
（3）瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣，决定从三项活动中随机抽取一项参加，利用树状图或列表表示所有可能结果，并求出两人参加同一项目的概率；
（4）由于场地限制，参加足球活动的学生人数不能超过参加其余活动学生人数的 ，那么至少几位同学需要从参加足球活动调整到参加其余活动？

【题目】某地电话拨号上网有两种收费方式，用户可以任选其一：

（A）计时制，0.08元/分；

（B）包月制，50元/月（限一部个人住宅电话上网）；

此外，每种上网方式都附加通信费0.02元/分．

（1）某用户某月上网时间为x分钟，则该用户在A、B两种收费方式下应支付费用各多少元？

（2）如果一个月内上网200分钟和300分钟，按两种收费方式各需交费多少元？

（3）是否存在某一时间，会出现两种收费方式一样的情况？如果存在，请求出这时的上网时间．

【题目】如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；

（1）若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；

（2）若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．

【题目】已知：如图，在△ABC中，AB＝AC，AD是△ABC的一条角平分线，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E.

(1)求证：四边形ADCE为矩形；

(2)连接DE，交AC于点F，请判断四边形ABDE的形状，并证明；

(3)线段DF与AB有怎样的关系？请直接写出你的结论．

【题目】如图，已知反比例函数y=﹣ 的图象与直线y=kx（k＜0）相交于点A、B，以AB为底作等腰三角形，使∠ACB=120°，且点C的位置随着k的不同取值而发生变化，但点C始终在某一函数图象上，则这个图象所对应的函数解析式为 ．

【题目】如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点(点M不与B、C重合)，过点C作CN垂直DM交AB于点N，连结OM、ON、MN.下列五个结论：①△CNB≌△DMC；②；③ON⊥OM；④若AB＝2，则的最小值是1；⑤.其中正确结论是_________.(只填番号)

【题目】如图，反比例函数与一次函数的图象交于点A（－2，6）、点B（，1）.

（1）求反比例函数与一次函数的表达式；

（2）点E为y轴上一个动点，若S△AEB=5，求点E的坐标．

（3）将一次函数的图象沿轴向下平移n个单位，使平移后的图象与反比例函数的图象有且只有一个交点，求n的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网