题目内容
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.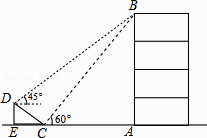
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
【答案】
(1)
解:在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,
∴DE= ![]() DC=2米;
DC=2米;
(2)
解:过D作DF⊥AB,交AB于点F,
∵∠BFD=90°,∠BDF=45°,
∴∠BFD=45°,即△BFD为等腰直角三角形,
设BF=DF=x米,
∵四边形DEAF为矩形,
∴AF=DE=2米,即AB=(x+2)米,
在Rt△ABC中,∠ABC=30°,
∴BC= ![]() =
= ![]() =
= ![]() =
= ![]() 米,
米,
BD= ![]() BF=
BF= ![]() x米,DC=4米,
x米,DC=4米,
∵∠DCE=30°,∠ACB=60°,
∴∠DCB=90°,
在Rt△BCD中,根据勾股定理得:2x2= ![]() +16,
+16,
解得:x=4+4 ![]() ,
,
则AB=(6+4 ![]() )米.
)米.
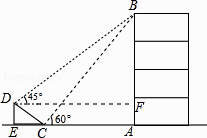
【解析】(1)在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设BF=DF=x,表示出BC,BD,DC,由题意得到三角形BCD为直角三角形,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出AB的长.

 名校课堂系列答案
名校课堂系列答案【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
| 250 |
x |
|
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.