Question

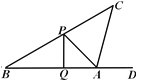
【题目】如图所示，⊙D 的半径为3，A是圆D外一点且AD=5，AB，AC分别与⊙D相切于点B，C．G是劣弧BC上任意一点，过G作⊙D的切线，交AB于点E，交AC于点F．

（1）求△AEF的周长；

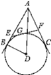
（2）当G为线段AD与⊙D的交点时，连结CD，则五边形DBEFC的面积是多少？．

Answer 1

【答案】(1)8;(2)9.

【解析】

（1）通过作辅助线，连接ED，DG，FD，CD，利用切线长定理就可证明BE=EG，FG=FC，则△AEF的周长是：AE+EG+FG+AF=AB+AC，据此即可求解；
（2）如图，当G为线段AD与⊙D的交点时，EF于AD垂直，根据△AEG∽△ADB求得EF的长，根据S五边形DBEFC=S四边形ABDC-S△AEF求解．

解：（1）如图1所示：连接ED，DG，FD，CD，

∵AB，AC分别与⊙D相切于点B，C，

∴AB=AC，∠ABD=∠ACD=90°，

∵⊙D 的半径为3，A是圆D外一点且AD=5，

∴AB=4，

∵过G作⊙D的切线，交AB于点E，交AC于点F，

∴BE=EG，FG=FC，则△AEF的周长是：AE+EG+FG+AF=AB+AC=8．

（2）如图2，AG=AD﹣DG=5﹣3=2．

∵在△AEG和△ADB中，∠ABD=∠AGD=90°，∠BAD=∠EAG，

∴△AEG∽△ADB，

∴，∴EG=，

∴EF=2EG=3，∴S△AEF=EF·AG=×3×2=3．

又∵S四边形ABDC=2S△ABD=ABBD=3×4=12，

∴S五边形DBEFC=12﹣3=9．