题目内容
【题目】如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中结论一定正确的序号数是( )
.其中结论一定正确的序号数是( )

A. ①② B. ①③ C. ③④ D ②④
【答案】B
【解析】①由于∠A=60°;在△ABC中,∠ABC+∠ACB=180°-∠A=120°,即∠FBC+∠FCB=60°,而∠BFE正好是△BFC的外角,即∠BFE=∠FBC+∠FCB=60°所以![]() ,故正确;
,故正确;
②若BC=BD,需满足一个条件:∠BCD=∠BDC,且看这两个角的表达式:∠BCD=180°-∠A-2∠DBA=120°-2∠DBA;∠BDC=∠BDA+∠A=60°+∠DBA;联立两式,可得∠DBA=20°;此时∠ABC=40°,而没有任何条件可以说明∠ABC的度数是40°,即可得出本选项错误.
③由于F是∠ABC和∠ACB角平分线的交点,因此F是△ABC的内心,可过F作AB、AC的垂线,通过证构建的直角三角形全等,得出FE=FD的结论,因结论正确;
④若BF=2DF,则F是△ABC的重心,即三边中线的交点,而题目给出的条件是F是△ABC的内心,显然两者的结论相矛盾,因此不正确.
所以本题正确的结论:①③.
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 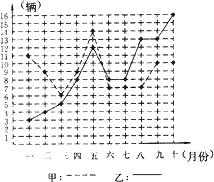
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).

