��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У���P������Ϊ�� ![]() ������Q������Ϊ
������Q������Ϊ ![]() ����
���� ![]() ��
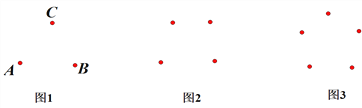
�� ![]() ����P��QΪij�����ε��������㣬�Ҹþ��ε�һ��Ա���ij��������ƽ�У���Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ���ͼ2��ͼ3�е�A������Ϊ��4,3��.
����P��QΪij�����ε��������㣬�Ҹþ��ε�һ��Ա���ij��������ƽ�У���Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ���ͼ2��ͼ3�е�A������Ϊ��4,3��.
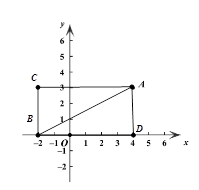
��1������B������Ϊ��-2,0�������A��B�ġ���ؾ��Ρ������Ϊ��
��2����C��y���ϣ�����A��C�ġ���ؾ��Ρ������Ϊ8����ֱ��AC�Ľ���ʽ��
��3����ͼ3��ֱ�� ![]() ��x�ύ�ڵ�M����y�ύ�ڵ�N����ֱ��MN���Ƿ���ڵ�D��ʹ��A��D�ġ���ؾ��Ρ�Ϊ�����Σ�������ڣ��������D�����꣬��������ڣ���˵������.
��x�ύ�ڵ�M����y�ύ�ڵ�N����ֱ��MN���Ƿ���ڵ�D��ʹ��A��D�ġ���ؾ��Ρ�Ϊ�����Σ�������ڣ��������D�����꣬��������ڣ���˵������.
���𰸡�
��1��18
��2��
�⣺�ɡ���ؾ��Ρ��Ķ��壬��C���A�ھ���������Եģ�
�ߵ�C��y���ϣ�����C��0��a����
��|a-3|��4=8�����a=1��5��
��C��0,1����0,5����
��C��0,1��ʱ��ֱ��AC�Ľ���ʽy= ![]() x+1��
x+1��
��C��0,5��ʱ��ֱ��AC�Ľ���ʽy= ![]() x+5.
x+5.
��3��
�⣺����.����D��x, ![]() ��,
��,
��A��D����ؾ���Ϊ������ʱ��
��|x-4|=| ![]() -3|��
-3|��
��x-4= ![]() -3����x-4=
-3����x-4= ![]()
���x=2��x=10.
��D��2,1����10,3��.
���������⣺��1����ͼ������ACBDΪA��B�ġ���ؾ��Ρ���
���������4+2����3=18.