Question

【题目】如图，直角梯形ABCD中，∠C=∠D=90°，AD＜BC，BC=CD=6，E是边CD上的一点，恰好使AE=5，并且∠ABE=45°，则CE的长是___________.

Answer 1

【答案】2或3

【解析】

过点B作BF⊥AD交DA的延长线于F，可得四边形BCDF是正方形，把△BCE绕点B顺时针旋转90°得到△BFG，根据旋转的性质可得CE=FG，BE=BG，∠CBE=∠FBG，然后求出∠ABG=45°，从而得到∠ABE=∠ABG，再利用“边角边”证明△ABE和△ABG全等，根据全等三角形对应边相等可得AE=AG，然后求出AF+CE=AE，设CE=x，表示出DE，再表示出AF、AD，然后在Rt△ADE中，利用勾股定理列出方程求解即可得到CE的长度．

解：如图，过点B作BF⊥AD交DA的延长线于F，

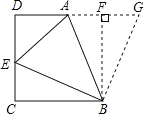
∵AD∥BC，∠D=90°，BC=CD，

∴四边形BCDF是正方形，

把△BCE绕点B顺时针旋转90°得到△BFG，则CE=FG，BE=BG，∠CBE=∠FBG，

∵∠ABE=45°，

∴∠ABG=∠ABF+∠FBG=∠ABF+∠CBE=90°-∠ABE=90°-45°=45°，

∴∠ABE=∠ABG，

在△ABE和△ABG中，

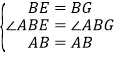
∴△ABE≌△ABG（SAS），

∴AE=AG，

∴AF+CE=AF+FG=AG=AE，

设CE=x，则DE=6-x，AF=5-x，

∴AD=6-（5-x）=x+1，

在Rt△ADE中，AD2+DE2=AE2，

即（x+1）2+（6-x）2=52，

整理得，x2-5x+6=0，

解得x1=2，x2=3，

所以CE的长度是2或3．