题目内容
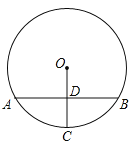
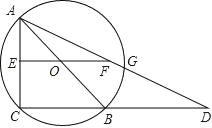
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,连接AC、CB,过O作EO∥CB并延长EO到F,使EO=FO,连接AF并延长,AF与CB的延长线交于D.求证:AE2=FGFD.
【答案】详见解析
【解析】
如图,连结BF、BG.由△AEO≌△BFO的对应边相等得到AE=BF,然后由圆周角定理和平行线的性质易证△FGB∽△FBD,则根据该相似三角形的对应边成比例证得结论.
证明:连结BF、BG.

∵在△AEO和△BFO中,
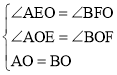 ,
,
∴△AEO≌△BFO(AAS),
∴AE=BF.
又∵∠ACB=90°,EF∥BC,
∴∠OFB=∠AEO=∠ACB=90°,
∴∠FBD=90°,
又∵BG⊥FD,
∴△FGB∽△FBD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AE2=FGFD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某单位现要组织其市场和生产部的员工游览该公园,门票价格如下:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1245元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为945元.那么该公司这两个部的人数之差的绝对值为_____.