题目内容
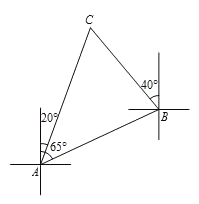
【题目】如图，正六边形
和正五边形
的
边重合，
的延长线与
交于点
，则
的度数是（ ）
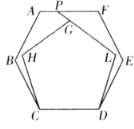
A.141B.144C.147D.150
【答案】B
【解析】
先根据多边形的内角和公式分别求得正六边形和正五边形的每一个内角的度数，再根据多边形的内角和公式求得∠APG的度数．
解：∵在正六边形ABCDEF中，
∠A＝∠B＝∠BCD＝（6－2）×180°÷6＝120°，
在正五边形GHCDL中，
∠L＝∠CDL＝（5－2）×180°÷5＝108°，
∴在六边形ABCDLP中，
∠APG＝（6－2）×180°－（∠A＋∠B＋∠BCD）－（∠L＋∠CDL）
＝（6－2）×180°－120°×3－108°×2
＝720°－360°－216°
＝144°．
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
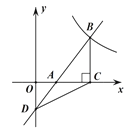
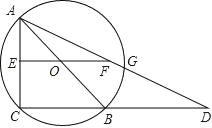
【题目】如图，⊙O的直径AB＝4cm，点C为线段AB上一动点，过点C作AB的垂线交⊙O于点D，E，连结AD，AE．设AC的长为xcm，△ADE的面积为ycm2．
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）确定自变量x的取值范围是 ；
（2）通过取点、画图、测量、分析，得到了y与x的几组对应值，如下表：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
（3）如图，建立平面直角坐标系xOy，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
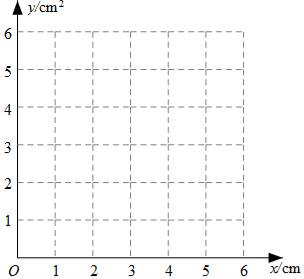
（4）结合画出的函数图象，解决问题：当△ADE的面积为4cm2时，AC的长度约为 cm．
