题目内容
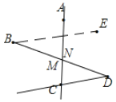
【题目】按要求画图：（1）如图1平面上有五个点
，按下列要求画出图形.
①连接
；
②画直线
交于点
；
③画出线段
的反向延长线；
④请在直线上确定一点
，使
两点到点的距离之和最小，并写出画图的依据.
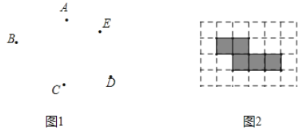
（2）有5个大小一样的正方形制成如图2所示的拼接图形（阴影部分），请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.（注意：只需添加一个符合要求的正方形，并用阴影表示）
【答案】（1）见解析；（2）见解析
【解析】
（1）根据几何语言画出对应的图形；连接BE交AC于N，则点N满足条件；
（2）结合正方体平面展开图的特征，只要折叠后能围成正方体即可．
解：（1）①②③如图所示；④连接BE交AC于N，N即为所求，依据：两点之间线段最短.
（2）如图所示．
练习册系列答案
阅读快车系列答案
相关题目
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛，学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试，他们各自的成绩（百分制）如表：
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
（1）由表中成绩已算得甲的平均成绩为80.25，请计算乙的平均成绩，从他们的这一成绩看，应选派谁；
（2）如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权，请分别计算两名选手的平均成绩，从他们的这一成绩看，应选派谁．
