题目内容
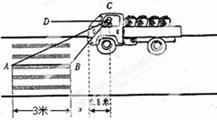
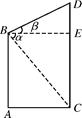
某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑,其横截面示意图如图所示.已知支架AC与斜坡AB的夹角为28°,支架BD⊥AB于点B,且AC、BD的延长线均过⊙O的圆心,AB=12m,⊙O的半径为1.5m,求雕塑最顶端到水平地面的垂直距离.(结果精确到0.01m)
(参考数据:cos28°≈0.9,sin62°≈ 0.9, sin44°≈0.7, cos46°≈ 0.7)
(参考数据:cos28°≈0.9,sin62°≈ 0.9, sin44°≈0.7, cos46°≈ 0.7)

10.83
试题分析:过点O作水平地面的垂线,垂足为E.
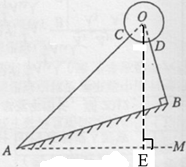
在RT△AOB中,cos∠OAB=
 ,即cos28°=
,即cos28°= =
=
所以
 =
=

因为∠EAB=16°,
所以∠OAE=28°+16°=44°.
在RT△AOE中,sin∠OAE

 ,即sin44°
,即sin44°
所以
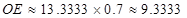 m
m 9.3333+1.5=10.83(米)
所以雕塑最顶端到水平地面的垂直距离约为10.83米.
点评:本题考查三角函数,解答本题需要掌握三角函数的定义,会根据三角函数的定义来解答本题

练习册系列答案
相关题目
 处测得树顶的仰角为
处测得树顶的仰角为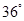 ,已知小明的眼睛(点
,已知小明的眼睛(点 )离地面约1.6m,求树的高度.(精确到0.1m)
)离地面约1.6m,求树的高度.(精确到0.1m)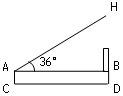
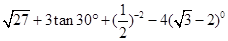 .
.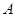 看地面
看地面 、
、 两点,测得它们的俯角分别是
两点,测得它们的俯角分别是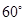 和
和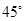 .已知
.已知 ,
,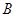 、
、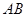 .(精确到
.(精确到 ,参考数据:
,参考数据: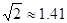 ,
,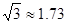 )
)