题目内容
如图,两座建筑物AB及CD,其中A,C距离为50米,在AB的顶点B处测得CD的顶部D的仰角β=30°,测得其底部C的俯角α=60°,求两座建筑物AB及CD的高度(精确到0.1米).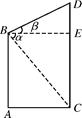

建筑物AB的高度约为86.6米,建筑物CD的高度约为115.5米.
试题分析:解:过点B作BE⊥CD,连结BC,
则∠α=60°,∠β=30°,
∵四边形ABEC是平行四边形
∴BE=AC=50,AB=CE
在Rt△BCE中,
∵tanα=
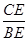
∴
 α=
α=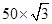 =
=
∴AB=
 ≈86.6(米)
≈86.6(米) 在Rt△BDE中,
∵tanβ=
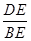
∴
 β=50
β=50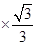 =
=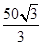
∴CD=CE+DE=
 +
+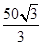 ≈115.5(米)
≈115.5(米) 答:建筑物AB的高度约为86.6米,建筑物CD的高度约为115.5米.
点评:本题难度中等,主要考查学生对三角函数解决实际问题综合运用能力。为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
相关题目


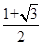
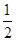 +
+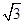
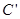 时,在A处又测得气球的仰角为30º,求CD与
时,在A处又测得气球的仰角为30º,求CD与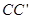 的长度.(结果保留根号)
的长度.(结果保留根号)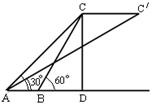
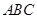 中,
中,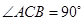 ,
,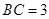 ,
,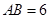 ,在
,在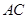 上取一点
上取一点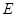 ,以
,以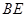 为折痕,使
为折痕,使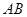 的一部分与
的一部分与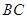 重合,
重合,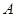 与
与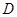 重合,则
重合,则 的长度为
的长度为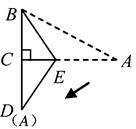
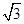
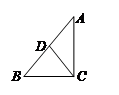
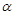 ,AB = 2,那么BC的长等于
,AB = 2,那么BC的长等于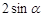
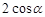
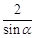
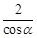
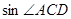 =( )
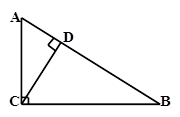
=( )
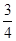
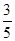
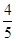
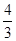
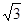 ,则边AB的长为______________。
,则边AB的长为______________。