题目内容
【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
(1)若点P恰好在∠ABC的角平分线上,求出此时t的值;
(2)若点P使得PB+PC=AC时,求出此时t的值.

【答案】(1)5;(2)![]()
【解析】
(1)作PD⊥AB于D,如图,AP=t,先利用勾股定理计算出AC=8,再根据角平分线的性质得到PC=PD=8-t,利用三角形面积公式得到![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,然后解方程即可;
×6×8,然后解方程即可;
(2)先证明PB=PA=t,再利用勾股定理得到(8-t)2+62=t2,然后解方程即可.
(1)作PD⊥AB于D,如图,AP=t,
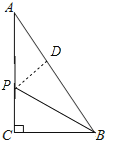
∵∠ACB=90°,AB=10,BC=6,
∴AC=![]() ,
,
∵BP平分∠ABC,
∴PC=PD=8-t,
∵S△ABP+S△BCP=S△ABC,
∴![]() ×10×(8-t)+
×10×(8-t)+![]() ×6×(8-t)=
×6×(8-t)=![]() ×6×8,
×6×8,
解得t=5,
即此时t的值为5;
(2)∵PB+PC=AC,PA+PC=AC,
∴PB=PA=t,
在Rt△BCP中,∵PC2+BC2=BP2,
∴(8-t)2+62=t2,解得t=![]() ,
,
即此时t的值为![]() .
.

练习册系列答案
相关题目