题目内容
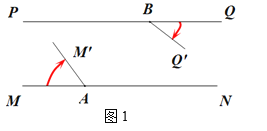
【题目】如图1，已知
，点
、
分别是直线
、
上的两点.将射线
绕点顺时针匀速旋转，将射线
绕点顺时针匀速旋转，旋转后的射线分别记为
、
，已知射线、射线旋转的速度之和为6度/秒.
（1）射线先转动
得到射线，然后射线、再同时旋转10秒，此时射线与射线第一次出现平行.求射线、的旋转速度；
（2）若射线、分别以（1）中速度同时转动
秒，在射线与射线
重合之前，设射线与射线交于点
，过点作
于点
，设
，
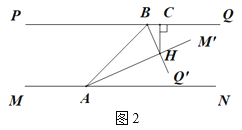
，如图2所示.
①当
时，求
、
、
满足的数量关系；
②当
时，求和满足的数量关系.
【答案】（1）射线
、
的旋转速度分别为5度/秒、1度/秒；（2）①当
时，
；②
.
【解析】
（1）设射线的旋转速度为
度/秒、则的旋转速度
度/秒,根据题意列出方程求解即可；
（2）①根矩，求出
，再根据
，求出
，即可求解；
②由（1）知射线、的旋转速度分别为5度/秒、1度/秒，可得
，
，再算
，再求出
即可求解.
解：（1）设射线的旋转速度为度/秒、则的旋转速度度/秒，
依题意得：
解得
∴
答：射线、的旋转速度分别为5度/秒、1度/秒.
（2）①∵
∴
∴
∵
∴
∴
∴
∴，
∴当时，
②由（1）知射线、的旋转速度分别为5度/秒、1度/秒
当射线、同时转动
秒后，
，，
∴
，
，
∴，
∵
，
∴
∵，
∴，又
∴
即.
练习册系列答案
一线名师权威作业本系列答案
相关题目
