题目内容
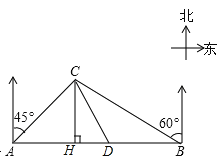
【题目】如图,把一副三角板如图甲放置,其中∠ACB=DEC=90°,∠A=45°,∠D=30°,AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙,这时AB与CD′相交于点O,D′E′与AB、CB分别相交于点F、G,连接AD′.

(1)求∠OFE′的度数;
(2)求线段AD′的长.
【答案】(1)120°(2)5cm
【解析】
试题分析:(1)由∠BCE′=15°,∠E′=90°,易得∠CGE′=∠FGB=75°,可得∠OFE1=∠B+∠FGB=45°+75°=120°;
(2)由∠OFE′=∠120°,得∠D′FO=60°,所以∠D′OF=90°,由AC=BC,AB=6cm,得OA=OB=OC=3cm,所以,OD′=CD′﹣OC=7﹣3=4cm,在Rt△AD′O中,AD′=![]() =
=![]() =5(cm).
=5(cm).
解:(1)由题意可知∠BCE′=15°,∠E′=90°,
∵∠CGE′=∠FGB,
∴∠FGB=75°,
∵∠B=45°,
∴∠OFE′=∠B+∠FGB=45°+75°=120°;
(2)∵∠OFE′=120°,∠CD′E′=30°,
∴∠D′OF=90°,
∵AC=BC,AB=6cm,OC⊥AB,
∴OA=OB=3cm,
∵∠OAC=45°,
∴∠OCA=45°,
∴OC=OA=3cm,
∵CD′=7cm,
∴OD′=4cm,
在Rt△AD′O中,
AD′=![]() =
=![]() =5(cm)
=5(cm)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目