题目内容
【题目】如图所示,![]() 是
是![]() 外一点,
外一点,![]() ,
,![]() 分别和
分别和![]() 切于
切于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 的切线分别交
的切线分别交![]() ,
,![]() 于
于![]() ,
,![]() .
.

![]() 若
若![]() 的周长为
的周长为![]() ,则
,则![]() 的长为________;
的长为________;
![]() 连接
连接![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的度数为________度.
的度数为________度.
【答案】5, 115
【解析】
(1)由于PA、PB、DE都是⊙O的切线,可根据切线长定理将△PDE的周长转化为切线PA、PB的长;
(2)根据切线长定理即可证得△PEF 周长等于2PA即可求解;根据切线的性质以及四边形的内角和定理即可求得∠AOB的度数,然后根据∠EOF=![]() ∠AOB即可求出∠BCA的度数.
∠AOB即可求出∠BCA的度数.
(1)∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
∴PA=PB=5;
(2)连接OA、OB、AC、BC,在⊙O上取一点F,连接AF、BF,
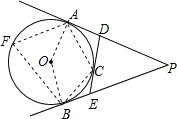
∵PA、PB分别切⊙O于A、B;
∴∠PAO=∠PRO=90°,
∴∠AOB=360°-90°-90°-50°=130°,
∴∠AFB=![]() ∠AOB=65°,
∠AOB=65°,
∵∠AFB+∠BCA=180°,
∴∠BCA=180°-65°=115°,
故答案是:5,115°.

练习册系列答案
相关题目
【题目】在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得x分,答错或不答扣y分,下表记录了其中两个参赛者的得分情况:
参赛者 | 答对题数 | 答错或不答题数 | 得分 |
A | 18 | 2 | 104 |
B | 13 | 7 | 64 |
(1)求出x和y的值;
(2)若参赛者C的得分要超过80分,则他至少要答对多少道题?






