题目内容
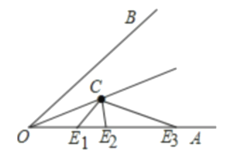
【题目】如图，∠AOB＝56°，OC平分∠AOB，如果射线OA上的点E满足△OCE是等腰三角形，那么∠OEC的度数为________________．
【答案】124°或76°或28°
【解析】
题目要求∠OEC的度数，而没有告诉∠OEC是等腰△OCE的顶角还是底角，由此此题要分类讨论;由角平分线的定义先求出∠AOC的度数，再分OE=CE、OC=CE、OE=OC进行讨论，结合等腰三角形的性质和三角形的内角和定理即可求出∠OEC的度数.
∵∠AOB=56°，0C平分∠AOB,
∴∠AOC=28°,
①当E在
时，OE=CE,
∵∠AOC=∠OCE=28°
∴∠OEC'=180°-28°-28°=124°，
②当E在
点时，OC=OE,可得：
③当E在
时，OC'=CE,
则∠OEC=∠A0C=28°,
故答案为: 124°或76°或28°.
【点睛]
本题考查等腰三角形内角的题目，解决本题的关键是结合等腰三角形的性质和三角形内角和定理解答.
练习册系列答案
相关题目
