题目内容
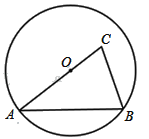
【题目】如图,AB是圆O的一条弦,点O在线段AC上,AC=AB,OC=3,sinA=![]() .求:(1)圆O的半径长;(2)BC的长.
.求:(1)圆O的半径长;(2)BC的长.
【答案】(1)5(2)![]()
【解析】
(1)过点O作OH⊥AB,垂足为点H,设OH=3k,AO=5k,则AH=![]() ,得到AB=2AH=8k,求得AC=AB=8k,列方程即可得到结论;
,得到AB=2AH=8k,求得AC=AB=8k,列方程即可得到结论;
(2)过点C作CG⊥AB,垂足为点G,在 Rt△ACG中,∠AGC=90°,解直角三角形即可得到结论.
(1)过点O作OH⊥AB,垂足为点H,
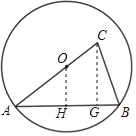
在 Rt△OAH中中,∠OHA=90°,
∴sinA=![]() ,
,
设OH=3k,AO=5k,
则AH=![]() ,
,
∵OH⊥AB,
∴AB=2AH=8k,
∴AC=AB=8k,
∴8k=5k+3,
∴k=1,
∴AO=5,
即⊙O的半径长为5;
(2)过点C作CG⊥AB,垂足为点G,在 Rt△ACG中,∠AGC=90°,
∴sinA=![]() ,
,
∵AC=8,
∴CG=![]() ,AG=
,AG=![]() ,BG=
,BG=![]() ,
,
在Rt△CGB中,∠CGB=90°,
∴BC=![]() .
.

练习册系列答案
相关题目