题目内容
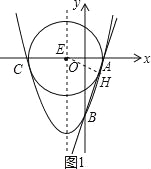
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=![]() +bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
(1)直接写出抛物线的解析式为 ;
(2)以点E为圆心的⊙E与直线AB相切,求⊙E的半径;
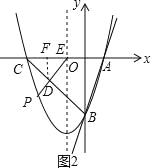
(3)连接BC,点P是第三象限内抛物线上的动点,连接PE交线段BC于点D,当△CED为直角三角形时,求点P的坐标.

【答案】(1)y=![]() +2x﹣3;(2)
+2x﹣3;(2)![]() ;(3)(﹣1,﹣4)或(
;(3)(﹣1,﹣4)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先利用一次函数解析式求出A点和B点坐标,再把A点和B点坐标代入y=![]() +bx+c得关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
+bx+c得关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)作EH⊥AB于H,如图1,先利用勾股定理计算出AB,再利用切线的性质得EH为⊙E的半径,然后证明Rt△EAH∽Rt△BAO,则可利用相似比计算出EH;
(3)先通过确定C点坐标可得到OC=OB=3,则可判断△OBC为等腰直角三角形,所以∠OCB=45°,分类讨论:当∠CDE=90°,则△CDE为等腰直角三角形,作DF⊥CE于F,如图2,根据等腰直角三角形的性质得DF=EF=CF=![]() CE=1,则可确定D(﹣2,﹣1),再利用待定系数法求出直线OD的解析式为y=x+1,然后通过解方程组
CE=1,则可确定D(﹣2,﹣1),再利用待定系数法求出直线OD的解析式为y=x+1,然后通过解方程组![]() 可得到此时P点坐标;当∠CED=90°时,EP∥y轴,此时P点为抛物线的顶点.
可得到此时P点坐标;当∠CED=90°时,EP∥y轴,此时P点为抛物线的顶点.
试题解析:(1)当y=0时,3x﹣3=0,解得x=1,则A(1,0),
当x=0时,y=3x﹣3=﹣3,则B(0,﹣3),
把A(1,0),B(0,﹣3)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得![]() ,
,
所以抛物线解析式为y=![]() +2x﹣3;
+2x﹣3;
故答案为:y=![]() +2x﹣3;
+2x﹣3;
(2)作EH⊥AB于H,如图1,
∵y=![]() +2x﹣3=
+2x﹣3=![]() ﹣4,
﹣4,
∴抛物线的对称轴为直线x=﹣1,则E(﹣1,0)
∵A(1,0),B(0,﹣3),
∴AB=![]() =
=![]() ,
,
∵以点E为圆心的⊙E与直线AB相切,
∴EH为⊙E的半径,
∵∠EAH=∠BAO,
∴Rt△EAH∽Rt△BAO,
∴EH:OB=EA:AB,即EH:3=2:![]() ,解得EH=
,解得EH=![]() ,
,
即⊙E的半径为![]() ;
;
(3)当y=0时,![]() +2x﹣3=0,解得
+2x﹣3=0,解得![]() =-3,
=-3,![]() =1,则C(﹣3,0),
=1,则C(﹣3,0),
∵OC=OB=3,
∴△OBC为等腰直角三角形,
∴∠OCB=45°,
当∠CDE=90°,则△CDE为等腰直角三角形,作DF⊥CE于F,如图2,则DF=EF=CF=![]() CE=1,
CE=1,
∴D(﹣2,﹣1),
设直线OD的解析式为y=mx+n,
把E(﹣1,0),D(﹣2,﹣1)代入得![]() ,解得
,解得![]() ,
,
∴直线OD的解析式为y=x+1,
解方程组![]() 得
得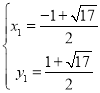 或
或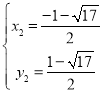 ,
,
∴P点坐标为(![]() ,
,![]() );
);
当∠CED=90°时,EP∥y轴,此时P点坐标为(﹣1,﹣4),
综上所述,满足条件的P点坐标为(﹣1,﹣4)或(![]() ,
,![]() ).
).

 阅读快车系列答案
阅读快车系列答案