题目内容
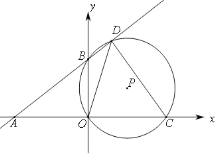
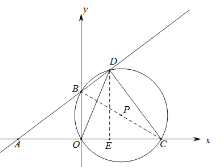
【题目】如图,直角坐标系中,直线![]() 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)![]() ;(2)D(
;(2)D(![]() ,
,![]() ).
).
【解析】
(1)把A、B两点坐标代入y=kx+b求出k、b的值即可;(2)连结BC,作DE⊥OC于点E,根据圆周角定理可得∠OBC=∠ODC,由tan∠ODC=![]() 可求出OC的长,进而可得AC的长,利用∠DAC的三角函数值可求出DE的长,即可得D点纵坐标,代入直线AB解析式求出D点横坐标即可得答案.
可求出OC的长,进而可得AC的长,利用∠DAC的三角函数值可求出DE的长,即可得D点纵坐标,代入直线AB解析式求出D点横坐标即可得答案.
(1)∵A(-8,0)、B(0,6)在y=kx+b上,
∴![]() ,
,
解得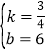 ,
,
∴直线AB的函数表达式为y=![]() x+6.
x+6.
(2)连结BC,作DE⊥OC于点E,
∵∠BOC=90°,
∴BC为⊙P的直径,
∴∠ADC=90°,
∵∠OBC=∠ODC,tan∠ODC=![]() ,
,
∴![]() ,
,
∵OB=6,OA=8,
∴OC=10,AC=18,AB=10,
∵cos∠DAC=![]() =
=![]() ,sin∠DAC=
,sin∠DAC=![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
∵D点在直线AB上,
∴![]() ,
,
解得:![]() ,
,
∴D(![]() ,
,![]() )
)

练习册系列答案
相关题目