��Ŀ����
����Ŀ���ס��������ֱ�����420km��A��B����������У��ҳ��ȼ׳��ȳ���1Сʱ�������ֱ��Ը��Ե��ٶ�������ʻ��;��C�أ�A��B��C������ͬһ��ֱ���ϣ����׳�����C�غ�������������ԭ·ԭ�ٷ���A�أ��ҳ���B��ֱ��A�أ��ס�����������Գ����ص�·��y��ǧ�ף���׳���ʻ���õ�ʱ��x��Сʱ���Ĺ�ϵ��ͼ��ʾ�����ͼ����Ϣ�ش��������⣺
��1���׳����ٶ����� ��ǧ��/ʱ���ҳ����ٶ����� ��ǧ��/ʱ��
��2����׳����������ص�·��y��ǧ�ף�������ʻ���õ�ʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3���׳������ʱ����������90ǧ�ף�����ֱ��д���𰸣�

���𰸡���1��105��60����2��y��![]() ����3��
����3��![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ʱ��
ʱ��
��������
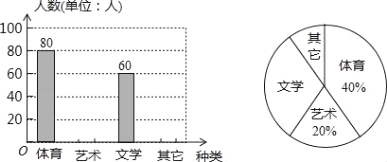
��1����������ͺ���ͼ���е����ݿ��Եõ������������ٶȣ�
��2����������ͺ���ͼ���е����ݿ�����ü׳����������ص�·��y��ǧ�ף�������ʻ���õ�ʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3�����������֪�����������90ǧ������������Ӷ����Խ���⣮
��1����ͼ�ɵã�
�׳����ٶ�Ϊ����210��2����4��420��4��105ǧ��/ʱ��
�ҳ����ٶ�Ϊ��60ǧ��/ʱ��
�ʴ�Ϊ��105��60��
��2����ͼ��֪����M������Ϊ��2��210����
��0��x��2ʱ����y��k1x��
��M��2��210���ڸú���ͼ���ϣ�
2k1��210��
��ã�k1��105��
��y��105x��0��x��2����
��2��x��4ʱ����y��k2x+b��
��M��2��210���͵�N��4��0���ڸú���ͼ���ϣ�
��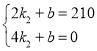 ����
����![]() ��
��
��y����105x+420��2��x��4����
�����������׳����������ص�·��y����������ʱ��x�ĺ�����ϵʽΪ��y��![]() ��
��
��3����׳�����aСʱʱ�������90ǧ�ף�
���״�A�ص�C��ʱ��
105a+60��a+1��+90��420��
��ã�a��![]() ��
��
���״�C�ط���A��ʱ��
��210��60��3��+��105��60������a��2����90��
��ã�a��![]() ��
��
������A�غ�
420��60��a+1����90��
��ã�a��![]() ��
��
�𣺼׳�����![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ʱ���������90ǧ�ף�
ʱ���������90ǧ�ף�