题目内容
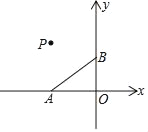
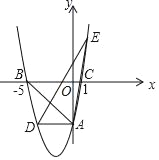
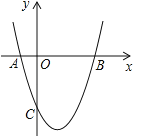
【题目】如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与
轴交于
点．
（1）求该抛物线的解析式；
（2）P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求点P的坐标；
（3）作直线BC，若点Q是直线BC下方抛物线上的一动点，三角形QBC面积是否有最大值，若有，请求出此时Q点的坐标；若没有，请说明理由．
【答案】（1）y=x2-2x-3；（2）P点的坐标为（ 0，
）或（ 0，
）；（3）点Q（
， - 
）．
【解析】
（1）把A（﹣1，0），B（3，0）两点代入y=-x2+bx+c即可求出抛物线的解析式；
（2）由A（﹣1，0），B（3，0）可得AB=4，由△PAB是以AB为腰的等腰三角形，可分两种情况PA=AB=4时，PB=AB=4时，根据勾股定理分别求出OP的长即可求解；
（3）由抛物线得C（0，-3），求出直线BC的解析式，过点Q作QM∥y轴，交BC于点M，设Q（x，x2-2x-3），则M（x，x-3），根据三角形QBC面积S=
QMOB得出二次函数解析式，根据二次函数的性质即可求出Q点坐标及△QBC面积的最大值
解：（1）因为抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，
所以可得
解得
．
所以该抛物线的解析式为：y=x2-2x-3；
（2）由A（﹣1，0），B（3，0）可得AB=4．
因为P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，可得PA=4或PB=4．
当PA=4时，因为A（﹣1，0），所以OP=
=，所以P（ 0，）；
当PB=4时，因为B（3，0），所以OP=
=，所以P（ 0，）；
所以P点的坐标为（ 0，）或（ 0，）；
（3）对于y=x2-2x-3，当x=0时，y= -3，所以点C（0，-3）
设直线BC的解析式为：y=kx+b（k≠0），B（3，0），C（0，-3）
可得
解得
所以直线BC的解析式为：y=x-3．
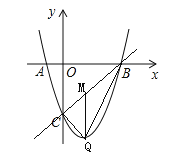
过点Q作QM∥y轴，交BC于点M，设Q（x，x2-2x-3），则M（x，x-3）．
所以三角形QBC的面积为S=QMOB=[（ x-3）-（x2-2x-3）]×3
= -x2+
x．
因为a=-<0，函数图象开口方向向下，所以函数有最大值，即三角形QBC面积有最大值．此时，x= -
=，此时Q点的纵坐标为-，所以点Q（，-）．
