题目内容
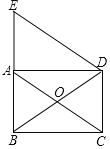
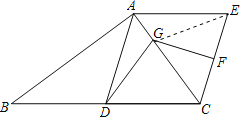
【题目】如图,在Rt△ABC中,AD为斜边BC上的中线,AE∥BC,CE∥AD,EC的垂直平分线FG交AC点G,连接DG,若∠ADG=24°,则∠B的度数为_____度.
【答案】38
【解析】
连接GE,证明四边形ADCE为菱形,得到∠DAC=∠EAC,根据△AGD≌△AGE得到∠AEG=∠ADG=24°,根据线段垂直平分线的性质得到GC=GE,根据等腰三角形的性质得到∠GEC=∠ECA,根据平行线的性质列式计算即可.
解:连接GE,
∵AE∥BC,CE∥AD,
∴四边形ADCE为平行四边形,
∵Rt△ABC中,AD为斜边BC上的中线,
∴AD=![]() BC=DC,
BC=DC,
∴平行四边形ADCE为菱形,
∴∠DAC=∠EAC,
在△AGD和△AGE中,
 ,
,
∴△AGD≌△AGE(SAS)
∴∠AEG=∠ADG=24°,
∵四边形ADCE为菱形,
∴∠DCA=∠ECA,
∵GF是EC的垂直平分线,
∴GC=GE,
∴∠GEC=∠ECA,
∵AE∥BC,
∴∠AEC+∠BCE=180°,
∴3∠ACB+24°=180°,
解得,∠ACB=52°,
∴∠B=90°﹣52°=38°,
故答案为:38.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目