题目内容
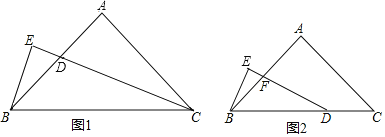
【题目】如图，在△ABC中，∠BAC=120°，将△ABC绕点A顺时针旋转一定角度（小于360°）得到△B′AC′．
（1）若点B′落在线段AC上，在图中画出△B′AC′，并直接写出当AC=4时，CC′的值；
（2）若∠ACB=20°，旋转后，B′C′⊥AC，请直接写出旋转角的度数．
【答案】（1）4
；（2）70°或250°．
【解析】
（1）如图1中，△B′AC′如图所示；作AH⊥CC′于H．只要证明CH=HC′，只要求出CH的长即可解决问题；
（2）如图2，分两种情况讨论．
（1）如图1中，△B′AC′如图所示；作AH⊥CC′于H．
∵AC=AC′=4，∠C′AC=∠CAB=120°，AH⊥CC′，∴CH=HC′，∠CAH=
∠CAC′=60°，∠ACH=30°，∴AH=AC=2，∴CH=
=2，∴CC′=4．
（2）如图2中，如图所示，分两种情况讨论：
①当B旋转到B′时．
∵B′C′⊥AC，∠C′=∠C=20°，∴∠C′AM=90°－∠C′=90°－20°=70°，∴旋转角为70°；
②当B旋转到B″时，同理可得：∠NAC″=70°．
∵∠B″AC″=∠BAC=120°，∴∠NAB″=120°－70°=50°．
∵∠BAN=180°－120°=60°，∴∠BAB″=60°+50°=110°，∴旋转角=360°－110°=250°．
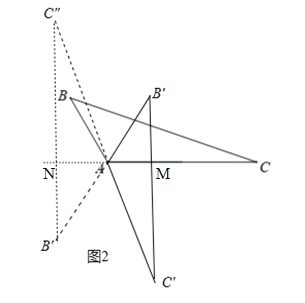
综上所述：旋转角的度数为70°或250°．
计算高手系列答案
【题目】“滴滴出行”改变了传统打车方式，最大化节省了司机与乘客双方的资源与时间．该打车方式的总费用由里程费和耗时费组成，其中里程费按
元
公里计算，耗时费按
元分钟计算．甲、乙两乘客用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与平均车速等信息如下表：
平均速度（公里/时） | 里程数（公里） | 车费（元） | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
（1）求，的值；
（2）如果你采用“滴滴出行”的打车方式，保持平均车速
公里时，行驶了
公里，那么你是否能够计算出打车的总费用？如果能，总费用为多少元？如果不能，请说明理由．
