题目内容
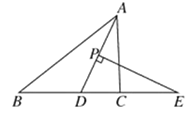
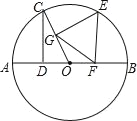
【题目】如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,且∠COD=60°,E为弧BC上一动点(不与点B、C重合),过E分别作于EF⊥AB于F,EG⊥OC于G.现给出以下四个命题:
①∠GEF=60°;②CD=GF;③△GEF一定为等腰三角形;④E在弧BC上运动时,存在某个时刻使得△GEF为等边三角形.
其中正确的命题是_____.(写出所有正确命题的序号)
【答案】①②④
【解析】
①根据四边形的内角和定理即可证到∠GEF=60°;②连接OE,取OE的中点O′,连接O′F,GO′,易证点E、G、O、F四点共圆,延长GO′交 O′于R,连接RF.利用三角函数可证到CD=GF;③运用反证法就可得到△GEF不一定为等腰三角形;④由于∠GEF=60°,要使得△GEF为等边三角形,只需要EG=EF即可,在 O′中只需∠COE=∠BOE即可,在 O中,只需点E在![]() 的中点即可.
的中点即可.
①∵EF⊥AB,EG⊥OC,
∴∠EGO=∠EFO=90°.
∴∠GEF+∠GOF=180°.
∵∠GOF=180∠COD=180°60°=120°
∴∠GEF=180°120°=60°.
故①正确.
②连接OE,取OE的中点O′,连接O′F,GO′,如图所示.
∵∠EGO=∠EFO=90°,点O′是OE的中点,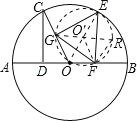
∴O′G=O′F=![]() OE.
OE.
∴点E.G、O、F在以点O′为圆心,O′O为半径的圆上.
延长GO′交O′于R,连接RF.
则有∠GRF=∠GEF=60°.
∵GR是O′的直径,∴∠GFR=90°.
∴GF=GRsin∠GRF=OEsin60°=![]() OE=
OE=![]() OC=CD.
OC=CD.
故②正确.
③假设△EGF一定是等腰三角形,
∵∠GEF=60°,∴△EGF一定是等边三角形.
∴EG与EF一定相等.
但E为弧BC上一动点(不与点B.C重合),显然EG与EF不一定相等.
∴假设不成立.
故③错误.
④当点E运动到![]() 的中点时,
的中点时,
则有∠COE=∠BOE.
∴EG=EF.
∵∠GEF=60°,
∴△EGF是等边三角形.
故④正确.
故答案为:①②④.

 阅读快车系列答案
阅读快车系列答案【题目】“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元
元![]() 公里计算,耗时费按
公里计算,耗时费按![]() 元
元![]() 分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:
分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:

平均速度(公里/时) | 里程数(公里) | 车费(元) | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
(1)求![]() ,
,![]() 的值;
的值;
(2)如果你采用“滴滴出行”的打车方式,保持平均车速![]() 公里
公里![]() 时,行驶了
时,行驶了![]() 公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.