题目内容
【题目】直线![]()
![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,以
两点,以![]() 为边向外作正方形
为边向外作正方形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,则过
,则过![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
【答案】![]()
【解析】
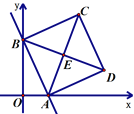
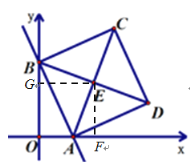
分别过点E作EF⊥x轴于F,过点E作EG⊥y轴于点G,再证明△BEG≌△AEF,得出EG=EF,从而可得出结论.
解:过点E作EF⊥x轴于F,过点E作EG⊥y轴于点G,
∵四边形ABCD为正方形,
∴BE=AE,且∠AEB=90°,
∴∠BEG+∠AEG=∠AEG+∠AEF,
∴∠BEG=∠AEF,
又∠BGE=∠AFE=90°,
∴△BEG≌△AEF(ASA),
∴EF=EG.
所以设过OE两点的直线的函数解析式为y=kx(k≠0),点E的坐标为(a,a),
代入可得a=ak,解得k=1,
∴过![]() 两点的直线的解析式是为y=x.
两点的直线的解析式是为y=x.
故答案为:y=x.

练习册系列答案
相关题目