题目内容
【题目】已知:如图,AC∥BD,折线AMB夹在两条平行线间.(1)判断∠M,∠A,∠B的关系;(2)请你尝试改变问题中的某些条件,探索相应的结论.建议:①折线中折线段数量增加到n条(n=3,4,…);
②可如图1,图2,或M点在平行线外侧.

【答案】见解析
【解析】
试题(1)过点M作ME∥AC,再根据平行线的性质进行解答即可;
(2)根据题意可假设点M在平行线外,画出图形,再根据平行线的性质及三角形内角和定理求解.
试题解析:
(1)过点M作ME∥AC,
∵AC∥BD,
∴AC∥BD∥ME,
如图1所示:
∵AC∥ME,
∴∠A=∠1,
∵BD∥ME,
∴∠B=∠2,
∴∠1+∠2=∠A+∠B,即∠AMB=∠A+∠B;
如图2所示:
∵AC∥ME,
∴∠A+∠3=180°,
∵BD∥ME,
∴∠B+∠4=180°,
∴∠A+∠B+∠3+∠4=360°,即∠A+∠B=360°-∠AMB;
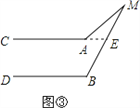
(2)如图③所示:
延长CA交BM于点E,
∵AC∥BD,
∴∠B=∠AEM,
∵∠CAM是△AEM的外角,
∴∠M+∠B=∠CAM.
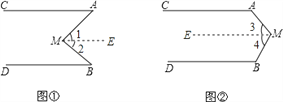

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目