题目内容
【题目】―抛物线与x轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)．
(1)求该抛物线的解析式；
(2)求该抛物线的顶点坐标．
【答案】(1) y＝2x2＋2x－4(2)(－
，－ 
)
【解析】分析:（1）因为已知抛物线与x轴两交点坐标，则设交点式y=a(x+2)(x-1，然后把c(2,8代入求出a即可；（2）把（1）中的函数解析式转化为顶点式，可以直接得到答案.
本题解析：
(1)设这个抛物线的解析式为y=ax2＋bx＋c．将A(－2，0)，B(1，0)，C(2，8)三点代入，得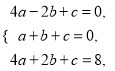
解这个方程组，得
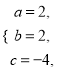∴所求抛物线的解析式为y＝2x2＋2x－4． (2)∵y=2x2＋2x－4＝2(x2＋x－2)=2(x＋
)2－
，∴该抛物线的顶点坐标为(－
，－ 
)．
练习册系列答案
精英口算卡系列答案
相关题目
