��Ŀ����
����Ŀ���Ķ����⣺
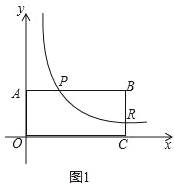
����������y=![]() ��k��0����һ�����ڵ�ͼ����ͼ1��ʾ����P��R��˫�����ϲ�ͬ�����㣬����P��R�ֱ���PA��y���ڵ�A��RC��x���ڵ�C�������߽���ΪB��
��k��0����һ�����ڵ�ͼ����ͼ1��ʾ����P��R��˫�����ϲ�ͬ�����㣬����P��R�ֱ���PA��y���ڵ�A��RC��x���ڵ�C�������߽���ΪB��
��1������������߶�PB��PA��BR��RC�������Ĺ�ϵ��
�����������PA=n��PB=m�����P��������n��![]() ������R��������m+n��
������R��������m+n��![]() ����AO=BC=
����AO=BC=![]() ��RC=
��RC=![]() ��BR=
��BR=![]()
![]() =
=![]()
��BR��RC=![]()
![]() ��
��
PB��PA=![]()
��PB��PA=BR��RC��
����Ӧ�ã�
��2����������Ľ��۽�����⣺
����ͼ1�����BR=6��CR=3��AP=4��BP=_____��
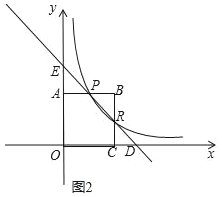
����ͼ2�����ֱ��PR�Ĺ�ϵʽy2=��x+3����x�ύ�ڵ�D����y�ύ�ڵ�E����ED=3PR�����k��ֵ��
���𰸡���.8;��k=2.
��������
��ֱ��������Ŀ�еĽ��ۼ������BP�ij���
������ֱ��DE�������Կ����AE=AP=BP=RC=CD�����֤�á�APE�ա�CDR��BPR���ɵõ�AP=BP=CD��������P�����꣬�����k��ֵ��
��������ɵã�![]() ����
����![]() ����ã�PB=8��
����ã�PB=8��
�ڡ�y2=-x+3,
��E��0,3��,D(3,0),
��OE=3,OD=3,
���AEP=��APE=��BPR=��BRP=��CRD=��CDR=45�㣬
��AE=AP��BP=BR��CD=CR��
��![]() ��
��
��AP=CR=AE=CD��
��ED=3PR��
��EP=RD=PR��
���APE�ա�CDR�ա�BPR��
��AP=BP=CD��
��OA=2��AP=1��
��P��1��2����
�ߵ�P��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��k=2.

����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
| �� |
|
|
|
|
| �� |
| �� |
|
|
|
|
| �� |
С�Ϲ۲��ϱ����ó�������ۣ�����������![]() ���һ������Ϊ
���һ������Ϊ![]() ��������
��������![]() �����ֵΪ
�����ֵΪ![]() ���������ߵĶԳ�����
���������ߵĶԳ�����![]() �����ڶԳ�����࣬
�����ڶԳ�����࣬![]() ��
��![]() ���������������ȷ�У� ��
���������������ȷ�У� ��
A. 0�� B. 1�� C. 2�� D. 3��



