题目内容
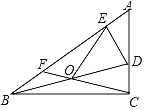
【题目】如图,在△ABC中,∠BCA=90°,D为AC边上一动点,O为BD中点,DE⊥AB,垂足为E,连结OE,CO,延长CO交AB于F,设∠BAC=α,则( )
A.∠EOF=![]() αB.∠EOF=2α
αB.∠EOF=2α
C.∠EOF=180°﹣αD.∠EOF=180°﹣2α
【答案】B
【解析】
设∠ABD=β,则∠BDC=∠ABD+∠A=β+α,由直角三角形的性质可得OE=![]() BD=OD,OC=OD,然后再根据等腰三角形的性质和三角形的内角和定理表示出∠EOD和∠COD,最后根据角的和差即可解答.
BD=OD,OC=OD,然后再根据等腰三角形的性质和三角形的内角和定理表示出∠EOD和∠COD,最后根据角的和差即可解答.
解:设∠ABD=β,则∠BDC=∠ABD+∠A=β+α,
∵DE⊥AB,
∴∠BED=90°,
∴∠BDE=90°﹣β,
∵O为BD中点,
∴OE=![]() BD=OD,
BD=OD,
∴∠OED=∠ODE,
同理得OC=OD,
∴∠OCD=∠ODC=α+β,
∴∠EOD=180°﹣2(90°﹣β)=2β,∠COD=180°﹣2(α+β)=180°﹣2α﹣2β,
∴∠EOF=180°﹣∠EOD﹣∠COD=180°﹣2β﹣(180°﹣2α﹣2β)=2α;
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 9 | 8 | 8 | 7 |
乙 | 10 | 6 | 7 | 9 |
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.