题目内容
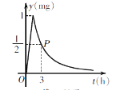
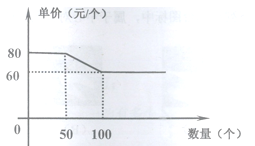
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具.两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
个.如果甲、乙两商店分别购买玩具,两商店需付款总和为y元.
(1)求y关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱;
(3)“六一”儿童节之后,该批发部对此玩具价格作了如下调整:数量不超过100个时,价格不变;数量超过100个时,每个玩具降价a元.在(2)的条件下,若甲、乙两商店“六一”儿童节之后去批发玩具,最多可节约2800元,求a的值.
【答案】(1)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时, ![]() ;(2)最多可节约9040-7200=1840元;(3)a=8.
;(2)最多可节约9040-7200=1840元;(3)a=8.
【解析】分析:
(1)设玩具的批发价为m,购买的数量为n,则由已知条件易得![]() (
(![]() );由题意可得
);由题意可得![]() ,由此可得
,由此可得![]() ,然后分①
,然后分①![]() ;②
;②![]() 两种情况结合已知条件求出y与x的函数关系式即可;
两种情况结合已知条件求出y与x的函数关系式即可;
(2)由题意将(1)中所得当![]() 时所得的函数关系式配方,即可求得两个商店分别购买所需资金的最大量,再由已知条件计算出两个商店联合购买所需的资金两,两者比较,即可得到所求的值;
时所得的函数关系式配方,即可求得两个商店分别购买所需资金的最大量,再由已知条件计算出两个商店联合购买所需的资金两,两者比较,即可得到所求的值;
(3)由题意可知,单独购买时,所需的最大金额不变,而联合购买所需资金为:120(60- a)=7200-120a,由题意可得:9040-(7200-120a)=2800,解此关于a的方程即可求得所求的值.
详解:
(1)由图可设玩具批发价m,数量为n,则m=kn+b(![]() ),
),
把 (50,80),(100,60)代入可求得![]() .
.
由题意得![]() ,解得
,解得![]() .
.
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时, ![]() .
.
(2)∵甲商店数量不超过100个,∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() .
.
∴x=70时,y最大值=9040(元).
两商店联合购买需120×60=7200(元),
∴最多可节约9040-7200=1840(元).
(3)单独购买不变,联合购买需120(60- a)=7200-120a(元),
∴9040-(7200-120a)=2800,解得a=8.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案